Question 1165474: Find the equation of the ellipse whose center is at (-3, -1), vertex at (2, -1), and focus at (1, -1).
a. (9x)2 + (36y)2 - 54x + 50y - 116 = 0
b. (4x)2 + (25y)2 + 54x - 50y - 122 = 0
c. (9x)2 + (25y)2 + 50x + 50y + 109 = 0
d. (9x)2 + (25y)2 + 54x + 50y - 119 = 0
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation of the ellipse is:

given:
center is at ( , ,  )=> )=>  , , 
so far we have:

focus at ( , , ) )
vertex at ( , ,  ) )
The major axis a is the segment that contains both foci and has its endpoints on the ellipse. These endpoints are called the vertices. The 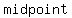 of the major axis is the of the major axis is the 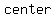 of the ellipse. of the ellipse.
so using midpoint formula, the other vertex will be at
 => => => => => => 
 => => => => => =>
other vertex will be at ( , , ) )
and the major axis = is distance between vertices is distance between vertices




so far


The formula generally associated with the focus of an ellipse is where where  is the distance from the focus to center , is the distance from the focus to center ,  is the distance from the center to a vetex and is the distance from the center to a vetex and 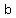 is the distance from the center to a co-vetex is the distance from the center to a co-vetex
if center is at ( , ,  ) and focus at ( ) and focus at ( , ,  ) )
and  is the distance from the focus to center, then=> is the distance from the focus to center, then=>
so,  and and





so, your equation is

expand:
 ... both sides multiply by ... both sides multiply by 
 ..........simplify ..........simplify






 => option d. => option d.
d. (9x)2 + (25y)2 + 54x + 50y - 119 = 0 -> should be 9x^2 + 25y^2 + 54x + 50y - 119 = 0
|
|
|