SOLUTION: circumference of the Earth the Greek mathematician Eratosthenes measured the circumference of the earth from the following observations. He noticed that on the certain day the sun

The Greek mathematician Eratosthenes was smart enough to INTERPRET these observations in a right way.


In Syene, the Eartn radius at that day and at that time was directed EXACTLY to the Sun.


In Alexandria, 500 miles North, the Earth radius (at the same day and the same time) made the angle of 7.2 degrees
with the direction to the Sun.


It means that the directions of the two radii made the angle of 7.2 degrees.


Then Eratosthenes used this equation for the arc of a circle

   S = .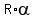


Here S is the arc length, R is the Earth radius (which should be evaluated/estimated), and   is the angle between two radii 
drawn to the arc's endpoints (central angle) in radians.



    (!) ancient Greeks and Egyptians just knew it at that time (!) (!)



In this equation,  S = 500 miles and   = 7.2 degrees = 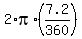 =  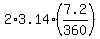= 0.1256 radians.


Thus  R = 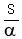 =  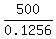= 3981 miles (rounded).


The contemporary value is R = 3959 miles

(see Wikipedia, https://www.google.com/search?q=the+eart+radius&rlz=1C1CHBF_enUS910US910&oq=the+eart+radius&aqs=chrome..69i57j0l7.6786j0j15&sourceid=chrome&ie=UTF-8 )


So, the Eratosthenes' estimate is very good (fantastically good, I'd say).