Question 116502: Pat and Jeff walked to a dock at 3mph, jumped into a boat, and motored to Dillion at 6mph. If the total distance was 24 miles and the trip took 4 3/4 hours in all, how far did they go by boat?
I realize this is a distance=rate x time, but don't know how to figure this out since we have a variable rate. Do you know the formula for this?
Found 2 solutions by ankor@dixie-net.com, solver91311:
Answer by ankor@dixie-net.com(22740)   (Show Source):
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! You are right about the formula being  , but you have to look at this as the sum of two separate trips, each part being described by the relationship .
First, the walking part. They traveled some part of 24 miles at 3 mph for some part of 4.75 hours.  .
Using a similar analysis, you can say:  to describe the boat part of the trip.
Since the entire trip was 24 miles, you can say that  , but  , so we can say:
Now we also know that  , which we can re-write as 
Now we can substitute this expression for  into the sum of distances equation:
And now all we need to do is simplify and solve for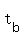 
Now we know that they were on the boat for 3.25 hours out of the total 4.75 hours, and we can put that back into the original boat trip equation to solve for  .
 . The boat trip was 19.5 miles.
Last step: VERY Important, Check Your Answer.
If the boat trip was 19.5 miles, the walk was 4.5 miles.
4.5 miles divided by 3 mph is 1.5 hours. 19.5 miles divided by 6 mph is 3.25 hours. 3.25 plus 1.5 = 4.75, so the answer checks.
Hope this helps
John
|
|
|
