SOLUTION: At noon, Terence and Linda drove from town A to town B. Terrence's avg speed for the whole journey was 15km/h faster than Linda's.when Terrence reached town B at 4 pm, Linda had o

Let d be the distance between the cities A and B.


Terence' traveled time was 4 hours (from noon till 4pm).

Hence, Terence' average speed was    hours.


It means that the Linda's average speed was 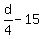  km/h  (15 km/h slower than that of Terence).


In 4 hours, from noon till 4 pm, Linda covered 224 kilometers.

It gives you this equation

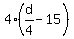     = 224,  or

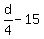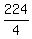     =  = 56.


Multiply both sides by 4 to get

    d - 60 = 56*4 = 224

    d = 224 + 60 = 284.


ANSWER.  The distance between the cities is 284 km.

Another way to solve this problem is to write so called  "speed equation"

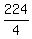     -  = 15


Saying that the difference between two speeds,    and 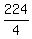  is 15 km/h.


Then from the equation you get

     - 56 = 15,

     = 15 + 56 = 71,

    d = 4*71 = 284,


giving the same answer.

The average speed of Linda is 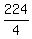  = 56 km/h.


The average speed of Terence is 15 km/h faster, i.e.  56+15 = 71 km/h.


Then the distance from A to B, which Terence covers in 4 hours, is  71*4 = 284 kilometers.