SOLUTION: Determine the present value of a series of 30 quarterly payments of $3,500 each which begins one month from today. Assume interest of 8.25 percent per year compounded monthly

In this tricky problem, we have quarterly payments of $3,500 each compounded monthly,
and the payments begin one month from today.


We are going to consider it as an Annuity Due saving plan, which starts one month from today.


But as given, in this problem the compounding is desynchronized with the payments.


There is a standard formula for the Future Value of an Annuity Due saving plan, but this formula 
was derived for synchronized payments and compounding.

Therefore, we want synchronize payments and compounding.


To synchronize them, we will introduce an equivalent effective quarterly compounding coefficient 
expressing it via the monthly compounding coefficient

    c = 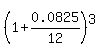 = 1.020767122.


Thus we will consider an equivalent scheme with quarterly compounding, synchronized with quarterly payments/deposits.


Then the Future Value of this equivalently modified account after 30 quarterly payments is calculated 
using the standard formula for Annuity Due saving plan

    FV =   dollars.


But remember that this formula gives the Future Value of the Annuity Due at the end 
of the Annuity Due saving plan, which happens 3 months after the last payment.

We, in opposite, want to know the amount of the account at the time of the last payment, 
i.e. 3 months before the end of the Annuity Due saving plan.


It makes clear, that to calculate the amount A(30) at the account at the last, 30-th payment, 
we should use the formula

    A(30) =  =  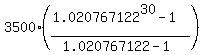= 143706.81 dollars.


Now we want to find the present value X.  It is the starting value of the other account (one-time deposit),
which, when compounded monthly at 8.25% per year, will generate the same value 
at the time of the 30-th payment, i.e. after 29 quarters PLUS 1 month = 3*29 + 1 = 88 months.


So, we write this equation

    143706.81 = .


It gives the solution

    X =  = 78637.24 dollars.


ANSWER.  The present value is $78,637.24.