Question 1164837: Mark left town P for town Q at 10am, travelling at a uniform speed of 75km/h. Jane left town P for town Q an hour after Mark, travelling at 120km/h. She passed Mark after travelling 2/5 of the journey. she reached town Q at 4 pm. How far was Jane from town Q when she passed Mark??
Found 3 solutions by ikleyn, greenestamps, MathTherapy:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
Mark left town P for town Q at 10am, travelling at a uniform speed of 75km/h.
Jane left town P for town Q an hour after Mark, travelling at 120km/h.
She passed Mark after travelling 2/5 of the journey. she reached town Q at 4 pm.
How far was Jane from town Q when she passed Mark?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
When Jane left town P for town Q at 11 am, Mark was 75 km ahead.
The difference of their speeds is 120 - 75 = 45 km/h.
Hence, Jane passed Mark in 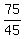 =  hours, counting from 11 am.
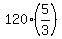During this time, hours, Jane covered the distance of  = 40*5 = 200 km.
This distance, 200 km, is  of the distance from P to Q, according to the problem.
Hence, the whole distance from P to Q is 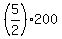 = 500 km.
From the other side, Jane traveled 5 hours (from 11 am to 4 pm) at the speed of 120 km/h -
hence, she traveled 5*120 = 600 km.
Thus we obtained two different values, 500 km and 600 km, for the distance from P to Q.
It tells us that the different parts of the problem are not consistent.
Thus, the problem is SELF-CONTRADICTORY, is posed INCORRECTLY and MAKES NO sense.
ANSWER. As presented in the post, the problem is SELF-CONTRADICTORY,
is posed INCORRECTLY and MAKES NO sense.
The problem in the post is composed in absolutely illiterate way.
All the accusations should be addressed to the problem's creator.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The given information is inconsistent, so the problem can't be solved.
Jane left at 11 am and arrived at 4 pm, traveling 5 hours at a speed of 120 km/hr, so the distance between the two towns was 120*5 = 600 km.
She passed Mark after traveling 2/5 of the way. 2/5 of 5 hours is 2 hours; 2/5 of 600 km is 240 km. So she passed Mark after traveling 240 km.
But Mark left 1 hour before Jane, so he traveled for 2+1 = 3 hours at 75 km/hr, traveling a distance of 3*75 = 225 km, by the time that Jane passed him.
And it is clearly impossible for Jane to have passed Mark when she 240 km and he was 225 km from their common starting point.
ANSWER: bad information; no solution
Answer by MathTherapy(10552)  (Show Source):
|
|
|
