Question 1164802: A bank loaned out $7,500, part of it at the rate of 14% annual interest, and the rest at 9% annual interest. The total interest earned for both loans was $825.00. How much was loaned at each rate?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
A bank loaned out $7,500, part of it at the rate of 14% annual interest, and the rest at 9% annual interest.
The total interest earned for both loans was $825.00. How much was loaned at each rate?
~~~~~~~~~~~~
Let x be the amount loaned at 14% annual interest.
Then the amount loaned at 9% interest is (7500-x) dollars.
The total interest equation is
0.14x + 0.09*(7500-x) = 825 dollars.
From the equation,
x = 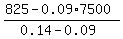 = 3000.
ANSWER. $3000 was loaned at 14% and the rest, 7500-3000 = 4500 dollars was loaned at 9%.
CHECK. 0.14*3000 + 0.09*4500 = 825 dollars. ! Correct !
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a quick and easy path to the solution, if a solution using formal algebra is not required.
$825 interest on $7500 is an interest rate of 825/7500 = 0.11 = 11%.
11% is 2/5 of the way from 9% to 14%.
Therefore, 2/5 of the money was loaned at the higher rate.
ANSWER: 2/5 of $7500, or $3000, at 14%; the other $4500 at 9%.
CHECK: .14(3000)+.09(4500) = 420+405 = 825
|
|
|
