Question 1164759: Determine the present value of a series of 30 quarterly payments of $3,500 each which begins one month from today. Assume interest of 8.25 percent per year compounded monthly.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the interest rate is compounded monthly.
8.25% / 12 = .6875% per month.
the investments of 3500 each are made once every 3 months beginning 1 month from now, and are made for 30 quarters which is equal to 90 months.
i believe that cash flow analysis using excel would be appropriate for this type of problem.
there may be another way, but i want to see what excel tells me before i attempt anything fancy using the present worth of an annuity formulas, because the excel analysis is probably the most straight forward and easy to understand.
i was able to duplicate the results using a financial calculator and some fancy footwork, but, as i said before, the excel net present value of a cash flow tool is the most straightforward.
i will show you what i did using the financial calculator so you can see what was done to make the results comparable.
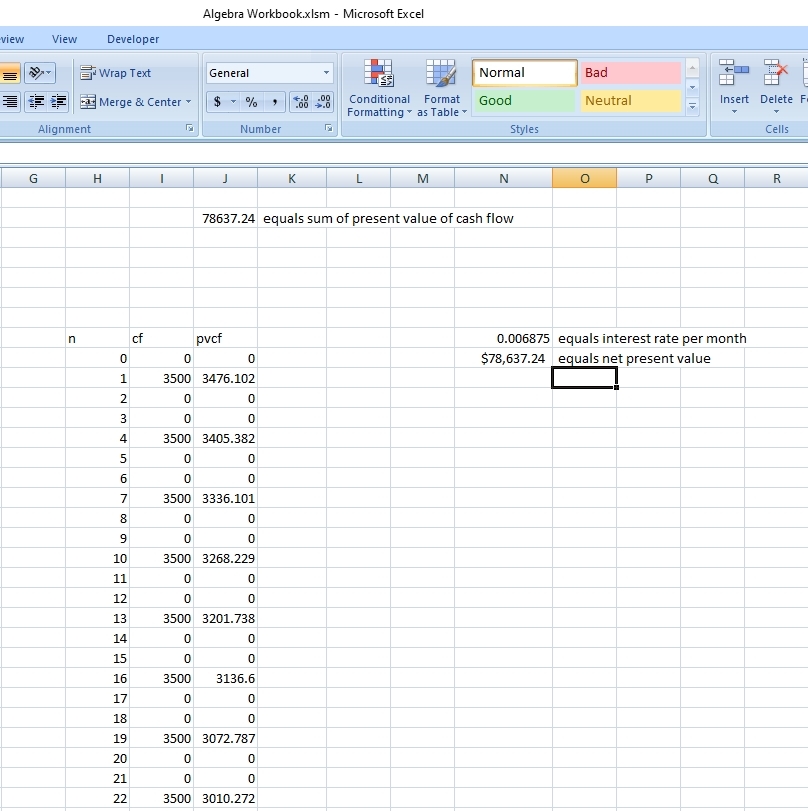
the results of the NPV (net present value) analysis of the cash flows using excel resulted in a net present value equal to $78,637.24.
here are the results from using excel.
here are the results from using the financial calculator at https://arachnoid.com/finance/index.html
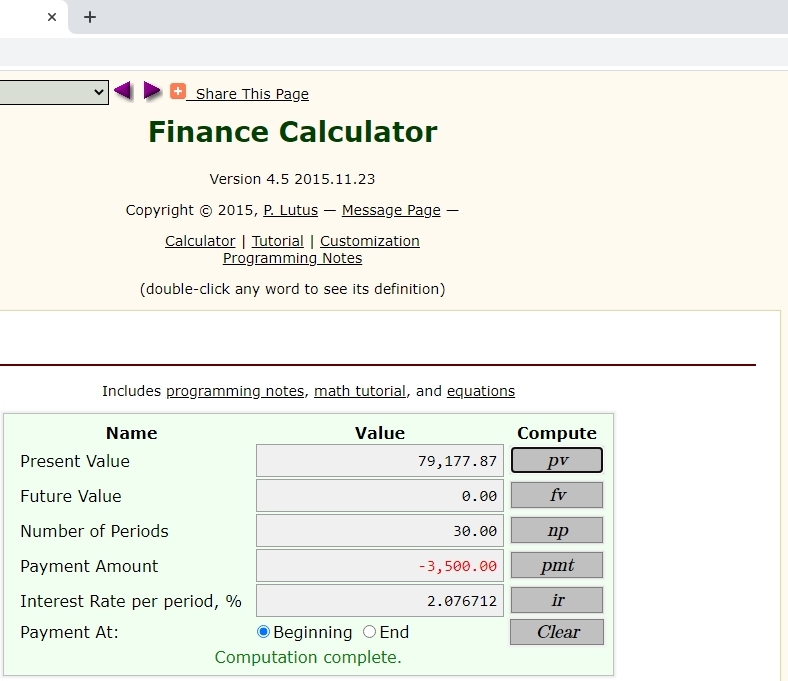
the results from the use of the financial calculator showed a present value of $79,177.87.
this is, however, a present value to the end of the first month.
to bring that back to the present value at the beginning of the first month, as i did with excel, it needed to be divided by (1 + .0825/12).
after doing this, the present value because 78,637.24.
this is the same as the net present value calculated through excel NPV of cash flow analysis.
for the net present value analysis using excel, the time periods are in months.
n = 0 is the beginning of the first month.
n = 1 is the end of the first month.
n = 2 is the end of the second month.
etc.
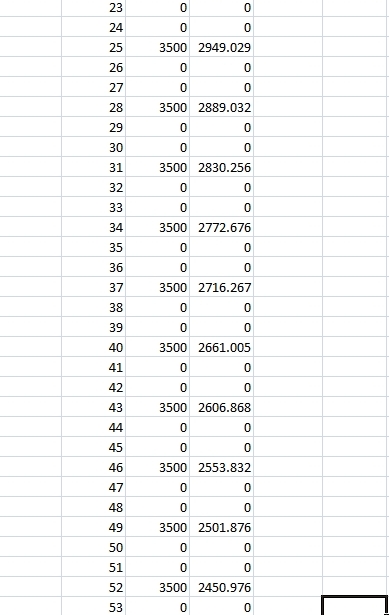
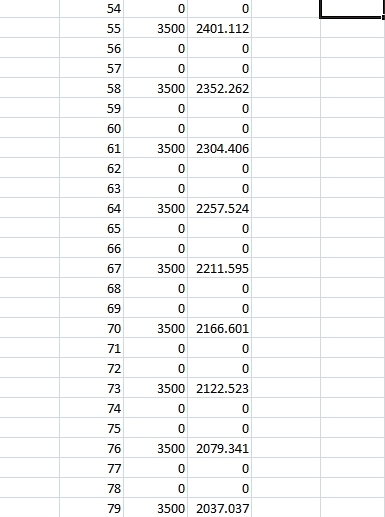
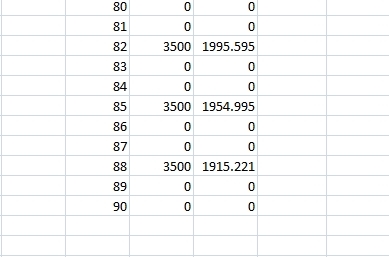
the cash flows of 3500 start at the end of the first month and continue every 3 months from there until 30 payments have been made.
the present value of the cash flow is the same as the net present value because they both do the same thing, i.e. the net present value is the present value of the cash flows at the indicated interest rate.
the interest rate used is .0825 / 12 = .006875.
to duplicate the results using the financial calculator, i had to convert the monthly interest rate into a quarterly interest rate.
since the compounding is per month, the monthly interest rate became 8.25% / 12 = .6875% per month.
to convert this to an equivalent quarterly interest rate i did the following.
(1 + .006875) ^ 3 = 1.020767122
subtract 1 from that and multiply it by 100 and you get a quarterly interest rate of 2.0767122%.
the calculator takes percents as input, while the excel analysis used the rate.
the rate is the percent divided by 100.
the percent is the rate * 100.
now that i got the equivalent quarterly rate, i made the following inputs to the calculator
present value = 0
future value = 0
number of time periods = 30 quarters of a year
payment amount is -3500.
interest rate percent per quarter is 2.076712%
payments are made at the beginning of each quarter.
i then clicked on PV and the calculator told me the present value was 79,177.87.
as i mentioned earlier, this present value is at the end of the first month.
i then divided it by (1 + .0825/12) to get it back to the beginning of the first month.
the present value became 78,637.24.
this is the same answer i got using excel.
the excel analysis was more straightforward.
the use of the financial calculator is ok as well as long as you know what you're doing.
the main thing using the financial calculator was to obtain the equivalent quarterly interest rate when the interest rate is compounded monthly.
since the yearly interest rate is compounded quarterly, than you take the yearly interest rate and divide it by 12.
that's how i got 8.25 / 12 = .6875%
that's the percent.
the rate is the percent rate divided by 100 = .006875.
to get the equivalent quarterly interest rate, you then had to add 1 to it and raise it to the 3d power (3 months in a quarter) to get (1.006875)^3 = 1.020767122.
you then had to subtract 1 from it and multiply it by 100 to get the percent.
you got 2.0767122%
that's what i entered into the financial calculator.
the display shows 2.076712.
that's just because the display has a limited number of digits to diaplay.
the input i made was 2.0767122.
both analyses got the same result.
i'm reasonably confident the results are correct.
hopefully you understand what was done and are able to duplicate the results on your own.
in the excel display:
n = the monthly time points
cf = cash flow
pvcf = present value of cash flow
npv = net present value
|
|
|