.
Suppose that A is a square matrix and  = 0 (the zero matrix). Show that
= 0 (the zero matrix). Show that
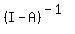 =
=  +
+  +
+ 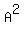 +
+  .
.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let B be the matrix  +
+  +
+ 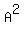 +
+  .
We need to show that (I-A)*B = I and B*((I-A) = I.
For the first equality, we have
(I-A)*B =
.
We need to show that (I-A)*B = I and B*((I-A) = I.
For the first equality, we have
(I-A)*B = 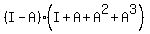 =
= 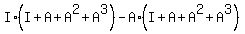 =
=
=
= 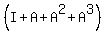 -
- 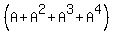 =
= 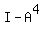 = I.
Here we used the fact that
= I.
Here we used the fact that  = 0, which is given.
Thus, the property (I-A)*B = I is proven.
For the second equality, we have
B*(I-A) =
= 0, which is given.
Thus, the property (I-A)*B = I is proven.
For the second equality, we have
B*(I-A) = 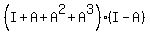 =
= 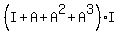 -
- 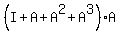 =
=
=
= 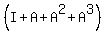 -
- 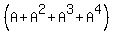 =
= 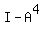 = I.
Again, here we used the fact that
= I.
Again, here we used the fact that  = 0, which is given.
Thus, the property B*(I-A) = I is proven.
= 0, which is given.
Thus, the property B*(I-A) = I is proven.
At this point, the problem is solved completely.