SOLUTION: The parabolic graph of the function f(x) = ax^2 + bx + c passes through the points with coordinates (1, 4), (2, 8), and (3, 14). Find a matrix equation for the coefficients a, b,

To get your first equation, substitute x= 1 into the formula (first point (1,4)).
You will get then

    f(1) = a*1^2 + b*1 + c = 4,   or

           a     + b   + c = 4.     (1)



To get your second equation, substitute x= 2 into the formula (second point (2,8)).
You will get then

    f(2) = a*2^2 + b*2 + c = 8,   or

           4a    + 2b  + c = 8.     (2)




To get your third equation, substitute x= 3 into the formula (third point (3,14)).
You will get then

    f(3) = a*3^2 + b*3 + c = 14,   or

           9a    + 3b  + c = 14.     (3)



In matrix form, your equation now is


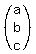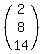           . = .     (4)



You should see the coefficients of the equations (1), (2) and (3) as the first, second and third rows 
of the coefficient matrix, respectively.


You also should see the right side terms of the equations (1,), (2) and (3) in the right side vector (4).