Question 1164209: Susan cashed a check at the bank, but the teller made a mistake. He gave her as many dollars as he should have given her cents and as many cents as he should have given her dollars. Susan took the money without realizing the error and spent $3.50. She then had twice as much money as the actual amount of the check. What was the amount of the check?
Found 5 solutions by ankor@dixie-net.com, Edwin McCravy, greenestamps, MathTherapy, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Susan cashed a check at the bank, but the teller made a mistake.
He gave her as many dollars as he should have given her cents and as many cents as he should have given her dollars.
Susan took the money without realizing the error and spent $3.50.
She then had twice as much money as the actual amount of the check.
What was the amount of the check?
;
let c = correct no. of cents
let d = correct no. of dollars
then
(d+.01c) = amt of the check
and
(c+.01d) = amt paid by teller
:
c + .01d - 3.50 = 2(d+.01c)
c + .01d - 3.50 = 2d + .02c
c -.02c + .01d - 2d = 3.50.
.98c - 1.99d = 3.50
Set up as an equation that we can graph on our calc and check the table
y=c; x=d
y = 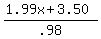
only one, two digit, integer solution
d = 14, c = 32
Actual check value: $14.32, teller paid $32.14
:
:
See if that checks out
$32.14
-3.50
-------
$28.64 which is twice $14.32
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by MathTherapy(10553)   (Show Source): (Show Source):
You can put this solution on YOUR website! Susan cashed a check at the bank, but the teller made a mistake. He gave her as many dollars as he should have given her cents and as many cents as he should have given her dollars. Susan took the money without realizing the error and spent $3.50. She then had twice as much money as the actual amount of the check. What was the amount of the check?
Let amount of dollars and cents he should’ve given her be D, and C, respectively
Therefore, he should’ve given her: “100D + C” cents
Then, he gave her C dollars and D cents, or “100C + D” cents
She spent $3.50, or 350 cents
Therefore, we get: 100C + D - 350 = 2(100D + C)
100C + D - 350 = 200D + 2C
100C - 2C = 350 + 200D - D
98C = 350 + 199D

Converting this to a DIOPHANTINE EQUATION, we get: 
Now, 2 * 98 = 196, and the integer that can be substituted for D in order to make 154 + 3D a DIVIDEND of 98 is 14. This gives us: 
So, with D being 14, we get: 
Therefore, D or number of dollars he should’ve given her was: 14, and number of cents he should’ve given her was: 32. Therefore, amount on check was: 
Answer by ikleyn(52807)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For linear Diophantine equations (one equation with integer coefficients for two integer unknowns) the trial an error method
finding a solution is absolutely and totally LEGAL (and standard) method.
For such equations, any version of trial and error search is ALLOWABLE, and nobody of mature mathematicians
do not really care by WHICH concretely searching method the solution is obtained.
You may use an Excel table/spreadsheet for it and to find the solution in seconds (as I usually do it . . . )
Nobody cares about it . . .
Or, alternatively, you can find it via 30 lines formula transformations. It is also good,
but again, NOBODY CARES about it . . .
What is REALLY IMPORTANT for such equations, it is the necessary and sufficient condition for  the solution. the solution.
This condition REQUIRES that the right side constant term must be a MULTIPLE of the Greatest Common Divisor of the coefficients
of the equation at "x" and "y".
If this condition is satisfied, then the solution DOES EXIST, and all the troubles just do stop at this point.
|
|
|