SOLUTION: A lizard jumps stright up from the ground. The lizard lands on a leaf that was directly above where it jumped from. Although the lizard jumped upward with an initial velocity of +8

To answer question (a), the physicist writes the energy conservation law equation


    mgh =  -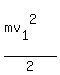 


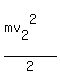saying the the potential energy increment mgh is the difference of the initial kinetic energy and the final kinetic energy.


Here m is the mass of the lizard, which we can cancel in both sides of the equation;

g is the gravity acceleration, g = 9.81 m/s^2, or 10 m/s^2 , approximately;

h is the difference of the levels  (= "how high above the grou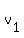nd");

  and 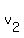   are the given velocities.



So, after canceling the mass "m" in both sides and substituting the given data, we get

    10h =  -  =  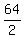-  = 32 - 2 = 30

      h                                     = 30/10 = 3.


So, the answer to the first question is "the leaf is 3 meters above the ground".




To answer question (b), physicist will use the base equation for a uniformly accelerated/decelerated move

     v = gt,


where v is velocity and t is the time ("g" is just introduced above).


The time for flying vertically up from the ground to the upperst possible height (till stop) is  

    t =  =  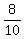= 0.8 seconds.


The time for falling down from the upperst height to get the speed of 2 m/s is

    t =  =  = 0.2 seconds.


The total time flying up and down is, thus,  0.8 + 0.2 = 1 second.