Question 1164031: Calculate each of the following. Your answer must be a number. No arithmetic operations are allowed in your answer. Please give 7 places after your decimal point if you use scientific notation.
a) 940!/(30! 910!)=
b) 290!/(255! 20!) =
c) (518 ! - 514 !)/515 ! =
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Making calculations is the students' honor duty and a privilege !
----------------
Below is my response to the Edwin's post.
Edwin, in your solution, you largely / widely use asymptotique formulas.
Asymptotics are not precise values, so you can not be sure and can not guarantee that your answer,
obtained with the use of asymptotics, is valid PRECISELY.
Therefore, I select another way.
First, it is clear to everybody that we can cancel factors 910! in the numerator and the denominator.
We get then widely known expression for binomial coefficient
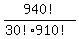 = = 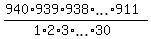 .
Next, it would be madness to calculate the products of 30 factors in the numerator and denominators SEPARATELY.
Instead, I will form the product of these 30 "local" ratios .
Next, it would be madness to calculate the products of 30 factors in the numerator and denominators SEPARATELY.
Instead, I will form the product of these 30 "local" ratios
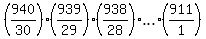 .
It is just VERY EASY to calculate it with Excel. The product and the answer is
3.6903095819*10^56.
+-----------------------------------------------------------------+
| It is really close to your result --- but using asymptotes, |
| you CAN NOT guarantee the precision, |
| |
| while I CAN, using my method. |
+-----------------------------------------------------------------+ .
It is just VERY EASY to calculate it with Excel. The product and the answer is
3.6903095819*10^56.
+-----------------------------------------------------------------+
| It is really close to your result --- but using asymptotes, |
| you CAN NOT guarantee the precision, |
| |
| while I CAN, using my method. |
+-----------------------------------------------------------------+
\\\\\\\\\\\\\\\\\
Edwin, I am very glad that you pointed/focused my attention on this calculation.
I think, that it would be EXTREMELY USEFUL for students to see HOW I do it and to learn from me.
Three points are key and are extremely important.
(1) Cancel all common factors in the numerator and denominator before going to massive calculations (!)
(2) Then present the ratio as the product of the small "local" ratios.
Do not neglect it (!) It is VERY IMPORTANT in such calculations (!)
(3) Do not use asymptotic formulas in these calculations : a) they are irrelevant, b) they do not provide
the precise answer and c) they even do not guarantee the needed precision to you (!)
And as a conclusion: This technique using these asymptotic formulas IS NOT ADEQUATE to the simplicity of the problem,
and I am 179% sure that these students never heard, never learned and know NOTHING about them.
/\/\/\/\/\/\/\/
Edwin, I worked for 40 years as a computer programmer - computational analyst - researcher, developing computer codes
and solving partial differential equations in 1D, 2D and 3D for heat transfer, thermal convection, radiation and hydrodynamics.
All these years I was in the front line . . .
So I know all the relevant theory and all the secrets and tricks in computational analysis (and all adjacent Mathematics).
And even much more behind, aside and around it . . .
So do not say please " @ikleyn missed something. "
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
|
|
|