SOLUTION: The function f : x ı→ a + b cos x, is defined for 0 ≤ x ≤ 2π. Given that f(0) = 10 and that f (2/3π)= 1 , find (i) the values of a and b, (ii)the range of f, (iii) th

You are given f(0) = 10.

Since  cos(0) = 1,  it means that

    a + b = 10.     (1)


It is your first equation to determine the unknown values of "a" and "b".


Next, cos(2/3π) = -0.5.

It gives you the second equation

    a - 0.5b = 1.    (2) 


Subtract equation (2) from equation (1).  You will get then

    1.5b = 10 - 1 = 9,

which implies  b = 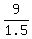 = 6.


Then from equation (1),  a = 10-6 = 4.


So, "a" and "b" are just found, and the answer to question (i) is  a= 4, b= 6.


So, your function is f(x) =  4 + 6*cos(x).


Next, since  -1 <= cos(x) <= 1,  it implies that  4 - 6 <= f(x) <= 4 + 6,   or  -2 <= f(x) <= 10.


In other words, the range of the function f(x) is the set of real numbers [-2,10].


It is the answer to question (ii).


Finally, the exact value of f(5/6π) is

    f(5/6π) = 4 + 6*cos(5/6π) = 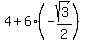 = 4 - 3*sqrt(3).


It is the answer to question (iii).


                    Visual check


    


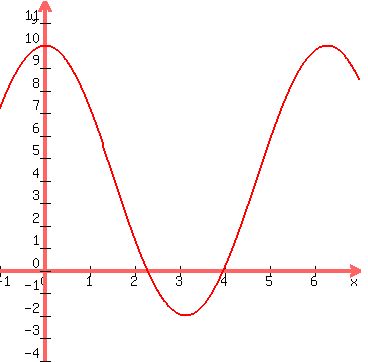                    Plot  y = 4 + 6*cos(x)