Question 1163952: 2 people walk towards each other on a road. It takes the first person 2 hours to walk the road, it takes the 2nd person 3 hours to walk the road. When they meet, the first person walked 4 and 4/5 of a mile more than the 2nd person. How long is the road?
Found 2 solutions by htmentor, ikleyn:
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first person's speed is s1 = d/2 (mi/h) where d is the total length of the road
The second person's speed is s2 = d/3 (mi/h)
The first person has walked a distance of d/2 + 4 4/5 when they meet
The second person has walked a distance of d/2 - 4 4/5 when they meet
Since they both walk for the same time, we can set the times equal to each other:
time = distance/speed
(d/2 + 4 4/5)/(d/2) = (d/2 - 4 4/5)/(d/3)
Solve for d: d + 48/5 = 3d/2 - 72/5
d/2 = 120/5 -> d = 48 mi
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two persons walk towards each other on a road. It takes the first person 2 hours to walk the road, it takes the 2nd person 3 hours to walk the road.
When they meet, the first person walked 4 and 4/5 of a mile more than the 2nd person. How long is the road?
~~~~~~~~~~~~~~~~
Since their times to cover the entire distance are in the ratio 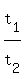 = =  , it means that their rates are in reciprocal ratio , it means that their rates are in reciprocal ratio 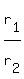 = =  .
In turn, it means that going toward each other, they cover the distances, whose ratio is the same as the ratio of their speeds, i.e. .
In turn, it means that going toward each other, they cover the distances, whose ratio is the same as the ratio of their speeds, i.e.  .
So, if "d" is the total one way distance, then the first person covered .
So, if "d" is the total one way distance, then the first person covered  of the distance, while the second covered of the distance, while the second covered  of the distance.
Then from the condition, you have this equation of the distance.
Then from the condition, you have this equation
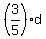 - - 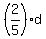 = =   miles, or miles, or
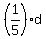 = = 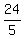 miles,
d = 24 miles. ANSWER miles,
d = 24 miles. ANSWER
Solved.
-------------
Notice that the solution by the tutor @htmentor is incorrect, since he incorrectly interprets the condition.
|
|
|