SOLUTION: there is a clock. The long and short hands are on a straight line. How long does it take for the 2 hands to overlap.

It is clear that the answer is the same for any possible positions of the two hands satisfying the given condition.


Therefore, let's assume that the initial position of the hands is 6:00 PM.


The minute hand is in position 90° vertically up.
The hour hand is in position -90° vertically down.


The angular speed of the minute hand is 360° per hour, or 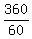  = 6 degrees per minute.

The angular speed of the hour   hand is 360° per 12 hours, or 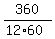  = 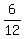 = 0.5 degrees per minute.


The position of the minute hand t minutes after 6:00 pm is  90 - 6t  degrees.

The position of the hour   hand t minutes after 6:00 pm is  -90 - 0.5t  degrees.


The hands overlap means

    90 - 6t = -90 - 0.5t,   or

    90 + 90 = 6t - 0.5t

    180     = 5.5t

    t  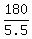   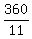  =  =  = 32.7272... minutes = 32 minutes 43.632 seconds, or approximately 32 minutes and 44 seconds.


So, the answer to the problem's question is 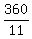  minutes, or 32 minutes and 44 seconds.