SOLUTION: 2 pipes fill up a pool. When both are used to fill water, it takes 1.2 hours to fill up the pool. If one is intake pipe and one is drainage pipe, it takes 6 hours to fill up the po

Let x be the rate of the first pipe and y be the rate of the second pipe.


    Notice that from the context, for each pipe, the rate filling is the same as the rate draining.


From the first condition,  the combined rate    x + y  is 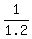  =  =   of the pool volume per hour.

From the second condition, the net inflow rate  x - y  is    of the pool volume per hour.


So you have this system of 2 equations

    x + y =     (1)

    x - y = .   (2)


Add the equations and get  2x = 1,  x = .


So, first pipe fills the pool in 2 hours, working alone.


Next, from equation (1)  

    y =  - x =  -  =  =  = .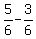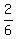


Hence, the second pipe fills the pool in 3 hours, working alone.