Question 1163797: If A and B work on a project, they need 8 1/9 days. A worked alone for 8 days then B worked alone for 10 days and finished the project. In how many days can A complete the project alone? B?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If A and B work on a project, they need 8 1/9 days. A worked alone for 8 days then B worked alone for 10 days
and finished the project. In how many days can A complete the project alone? B?
~~~~~~~~~~~~~
Let "a" be the rate of work of A, i.e. the part of work which A makes per day.
Let "b" be the rate of work of B, i.e. the part of work which B makes per day.
First statement of the problem says that the combined rate of work of A and B, working together,
is the value reciprocal to 8 = = 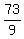 a + b =
a + b = 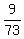 . (1)
The second statement of the problem says that
8a + 10b = 1. (2)
Thus the setup is completed, and you have now two equations for two unknowns "a" and "b".
To solve this system of equations, multiply equation (1) by 8 (both sides). Keep equation (2) as is.
You will get then
8a + 8b = . (1)
The second statement of the problem says that
8a + 10b = 1. (2)
Thus the setup is completed, and you have now two equations for two unknowns "a" and "b".
To solve this system of equations, multiply equation (1) by 8 (both sides). Keep equation (2) as is.
You will get then
8a + 8b = 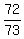 (3)
8a + 10b = 1 (4)
Next, subtract equation (3) from equation (4) (both sides). You will get
10b - 2b = 1 - (3)
8a + 10b = 1 (4)
Next, subtract equation (3) from equation (4) (both sides). You will get
10b - 2b = 1 - 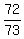 , or
2b = , or
2b = 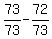 = =  .
Hence, b = .
Hence, b = 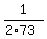 = = 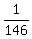 .
It means that B makes .
It means that B makes 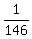 of the job per day; hence, B needs 146 days to complete the job alone.
Part of the problem is thus solved, and we need to find "a" now.
For it, from equation (2) you have
8a = 1 - 10b = 1 - of the job per day; hence, B needs 146 days to complete the job alone.
Part of the problem is thus solved, and we need to find "a" now.
For it, from equation (2) you have
8a = 1 - 10b = 1 - 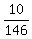 = = 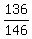 ;
hence, a = ;
hence, a = 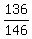 : 8 = : 8 = 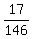 .
It means that A needs .
It means that A needs 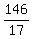 = 8 = 8 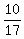 days to complete the job alone. days to complete the job alone.
Solved.
The numbers in the answer are ugly (at least one is ugly), but I checked them against the equations (1) and (2),
and the answer is CORRECT.
|
|
|