SOLUTION: There are 100 students enrolled in various AP courses at American High School. There are 31 students in AP European History, 52 students in AP Calculus, and 15 students in AP Span

You are given the sets 

    U - universal set of all 100 students
    H - set of students learning European History (31)
    C - set of students learning Calculus         (52)
    S - set of students learning Spanish          (15)

the in-pair intersections

    HC - History and Calculus                     (10)
    HS - History and Spanish                      ( 5)
    CS - Calculus and Spanish                     ( 8)

and the triple intersection

    HCS - History, Spanish and Calculus           ( 3)


For the union H U C S, there is a REMARKABLE formula from elementary set theory 


    n(H U C U S) = n(H) + n(C) + n(S) - N(HC) - n(HS) - n(CS) + n(HSC).    (1)


It says the number of elements in the union of three subsets is the alternate sum of the shown components.


By substituting the given values, you get the answer to the problem's question


    n(H U C U S) = 31 + 52 + 15 - 10 - 5 - 8 + 3 = 78.


So, 78 students learn at least one of the three subjects.


The rest 100-78 = 22 learn other subjects 


Therefore, the probability, the problem asks for is  P = 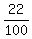 = 0.22.


ANSWER.  The probability that a student takes an AP course other than these three is 0.22.

    It is totally clear to you why I add the first three addends in the formula (1).

    But when I add them, I count twice every term in each in-pair intersection.

    Therefore, I subtract the numbers of terms in each in-pair intersection.

    Next, when I add three first addends, I count thrice each term in the triple intersection;

    and when I subtract in-pair intersections, I cancel these terms thrice.

    Therefore, I must add the number of terms in the triple intersection one more time to restore the balance.