Question 1163677: An escalator is moving up from first floor to the 2nd floor. If Marty stands on it, it takes 30 seconds to reach the 2nd floor. If he walks while the escalator is moving, it takes him 12 seconds. How long does it take if he walks up to the 2nd floor on the escalator while the escalator is not moving?
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let L be the escalator length, in some units of length.
Let "u" be the Marty's rate walking on unmoving escalator, in consistent units of length per second.
Let "v" be the escalator rate, in the same units.
Then from the condition,
L = 30*v (1) ("If Marty stands on it, it takes 30 seconds to reach the 2nd floor")
and
L = 12*(u + v) (2) ("If he walks while the escalator is moving, it takes him 12 seconds.")
From these equation
v = 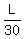 (3)
u + v = (3)
u + v =  (4)
Subtract equation (3) from equation (4). You will get
u = (4)
Subtract equation (3) from equation (4). You will get
u =  - - 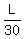 = =  = = 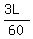 = = 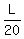 .
Thus we learned that the Marty' rate is .
Thus we learned that the Marty' rate is 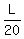 units of length per second.
The problem asks "how long does it take if he walks up to the 2nd floor on the escalator while the escalator is not moving".
This time is the distance L divided by the Marty' rate units of length per second.
The problem asks "how long does it take if he walks up to the 2nd floor on the escalator while the escalator is not moving".
This time is the distance L divided by the Marty' rate 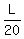 , i.e.
time = , i.e.
time = 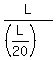 = 20 seconds. ANSWER
ANSWER. 20 seconds. = 20 seconds. ANSWER
ANSWER. 20 seconds.
Solved.
----------------
Do you understand the solution in full ?
In order for you do understand it even better, I will tell you that this "Travel & Distance" problem
is an exact analogue to "Joint work problem", where Marty is one of two participants and escalator is the other participant.
The distance L is then the job which they make together,
while their rates are "rates of work" in an corresponding "Joint work problem".
I recommend you to read and re-read this solution at least thrice.
|
|
|