Question 1163467: Sam drives from City A to City B, and he takes 8 hours for the entire trip.
Richard drives from City B to City A, and he takes 10 hours for the trip
assuming they are driving on the same road. If Sam leaves City A and Richard
leaves City B at the same time, how many hours will they meet at a place 40
km away from the halfway? Express your answer as a mixed number.
Found 3 solutions by ikleyn, Edwin McCravy, MathTherapy:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
On a highway, there are TWO such places/points that are 40 kilometers from the halfway between A and B.
I don't know who is a composer to this problem - you, or your professor, or a third party
(definitely it is not from a textbook, since textbooks are peer-reviewed), -
but it is composed VERY UNPROFESSIONALLY.
/\/\/\/\/\/
After reading the post by Edwin.
Edwin, I did not say "it is wrong", although it is.
I said "it is UNPROFESSIONAL", and it does not relate to the language (English, in this case), even.
Simply the formulation in the post is ACROSS of any human logic . . .
That is all . . .
The purpose of study Math is to develop the mind of a student.
It is the FIRST purpose, but not a unique.
The second purpose is to teach a student to formulate his (or her) thoughts in a proper logic form.
But as the problem is presented in the post, it is something out of human logic, whichever language (existing on the Earth) it would use.
Be sure, that I know how to re-formulate (or interpret) the problem correctly.
But in this forum, we have one (or several) visitors, who permanently produce
terrible Math problems formulations without having knowledge or experience on doing it properly.
I simply fight with them - I think that such persons should not litter the Internet with their production.
In the time of my studies in primary, secondary, high school and at the University, it was considered
as a greatest possible shame to bring or to publish incorrect or unclear Math problem, and a person
who admitted it, lost his reputation at the same day and forever.
OK, now I will show you on how the problem should be formulated in accurate way.
Sam drives from City A to City B, and he takes 8 hours for the entire trip.
Richard drives from City B to City A, and he takes 10 hours for the trip,
assuming they are driving on the same road. Sam leaves City A and
Richard leaves City B at the same time.
When they meet on a highway, they revealed that the meeting point was 40 km away from the halfway.
How many hours will did they drive to get this point ?
Express your answer as a mixed number.
Now the logic and the logical sequence / chain of events is in the place.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
I actually see nothing wrong with or unprofessional about the problem as
stated.
Ikleyn assumes all students who post here are from English-speaking
countries. It doesn't occur to her that often problems are the
student's own translations from other languages. So if a problem is not
stated in the best English, she will complain. Don't take it personally.
But, as I said above, I think the wording is OK.
What she didn't notice was that it's easy to tell which driver is
faster and thus which one will thus drive 40 km farther than halfway,
and which one is slower and will drive 40 km less than halfway.
Let x = distance from A to B (or B to A).
Sam drives from City A to City B, and he takes 8 hours for the entire trip.
Richard drives from City B to City A, and he takes 10 hours for the trip
assuming they are driving on the same road.
Make this chart, using rate = distance/time
| distance | rate | time |
--------------------------------------
Sam | x | x/8 | 8 |
Richard | x | x/10 | 10 |
Sam's rate is x/8 while Richard's rate is x/10.
If Sam leaves City A and Richard leaves City B at the same time, how many
hours will they meet at a place 40 km away from the halfway?
Let t = the time at which they meet.
Sam is faster, so he will travel 40 km farther than halfway, which is
1/2x+40.
Richard is slower, so he will travel 40 km less than halfway, which is
1/2x-40. Add those two lines onto the chart:
| distance | rate | time |
--------------------------------------
Sam | x | x/8 | 8 |
Richard | x | x/10 | 10 |
Sam | (1/2)x+40 | x/8 | t |
Richard | (1/2)x-40 | x/10 | t |
Use distance = rate × time to form two equations:
Multiply the first equation through by 8 and the second one
through by 10:
Since xt = xt, we have the equation:
4x + 320 = 5x - 400
720 = x
So the distance from A to B is 720 km.
Substitute 720 for x in:
That's the answer as a mixed number.
Edwin
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! Sam drives from City A to City B, and he takes 8 hours for the entire trip.
Richard drives from City B to City A, and he takes 10 hours for the trip
assuming they are driving on the same road. If Sam leaves City A and Richard
leaves City B at the same time, how many hours will they meet at a place 40
km away from the halfway? Express your answer as a mixed number.
Oh well, someone beat me to this one!!
Finding TIME, IMMEDIATELY
Since Sam takes 8 hours to complete the trip, while Richard takes 10 hours, “needless to say,” Sam’s speed is greater
than Richard’s, which means that Sam will get to the 40-km mark, on Richard’s side, after passing the ½-way mark
Let time taken by both to get to 40 kms beyond the ½-way point, from A, be T, and let distance from A to B, or from B to A, be 2D
Then the ½-way point is 2D/2 = D, and Sam will travel a distance of D + 40, while Richard will travel a distance of D - 40
Since Sam takes 8 hours to complete the trip, then Sam’s speed = 
Since Richard takes 10 hours to complete the trip, his speed, from B to A, is 
We then get the following SPEED equations for:
Sam and Richard
 
 ------ eq (i)  ------ eq (ii)
With  , and , we can say that: 
200(T - 4) = 160(5 - T) ------ Cross-multiplying
40(5)(T - 4) = 40(4)(5 - T)
5(T - 4) = 4(5 - T)
5T - 20 = 20 - 4T
5T + 4T = 20 + 20
9T = 40
T, or time taken by both to get to 40 kms beyond the ½-way point, from A is: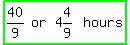 
OR
Finding Sam’s SPEED, in order to get the answer: TIME
Since Sam takes 8 hours to complete the trip, while Richard takes 10 hours, “needless to say,” Sam’s speed is greater
than Richard’s, which means that Sam will get to the 40-km mark, on Richard’s side, after passing the ½-way mark
Let Sam’s speed be S
Since Sam takes 8 hours to complete the trip, then distance, from A to B, or from B to A, is 8S
Since Richard takes 10 hours to complete the trip, his speed, from B to A, is 
As the distance is 8S, the ½-way point is:  , and with Sam’s speed being greater than Richard’s, Sam will travel to the 40-km mark, on “Richard’s side,” after passing the ½-way point.
As such, distance Sam will have traveled to get to 40 kms past the half-way point: 4S + 40, AND
distance Richard will have traveled to get to “Sam’s point”: 8S - (4S + 40) = 4S - 40
Time Sam takes to travel to 40 kms past the half-way point (on Richard’s side): 
Time Richard takes to travel to “Sam’s point”: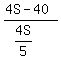 
Since they left at the same time, then their times will be the same, to get to "Sam's point." Therefore, we get:
4S + 40 = 5(S - 10) ------ Denominators are equal and so are the numerators
4S + 40 = 5S - 50
4S - 5S = - 50 - 40
- S = - 90
Sam’s speed, or 
Travelling 40 kms past the halfway mark (on “Richard’s side) - a distance of 4S + 40, or 4(90) + 40 = 400 kms, at S (90) km/h, or 400 km @ 90 km/h - time Sam takes is: 
OR
Travelling a distance of 4S - 40, or 4(90) - 40 = 320 kms, at  , or 320 kms @ 72 km/h - time Richard takes is: 
|
|
|
