SOLUTION: Two bicycles are driving on the circle in the same direction with speeds of 9 mph and 5 mph respectively. How many points are there on the circle where the two bicycles meet( and

Let  L  be the circumference of the circle.

Then the faster cyclist will catch the slower cyclist first time  when the faster cyclist will cover 
the distance which exactly 1 circumference longer than the distance covered by the slower cyclist 

      9t - 5t = L.


It gives the time to get first meeting point

       t =  =   hours


and the distance which the faster cyclist covered during this time is

        = 9t = 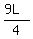  miles.


The distance which the slower cyclist covered during this time is 

        = 5t = .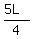


The meeting point is geometrically the same point on the circle for both cyclists, , 
and its angle measure on the circle is


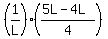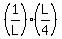         =  =  =   of the full angle of  radians, or 90 degrees.


So, they started simultaneously, and their first meeting point is at the 90 degrees angle.


Next, they started from this point  SIMULTANEOUSLY  and . . . and everything was repeated.


Hence, their next meeting point is the point on the circle with the angle of 180 degrees.



    It can be proved using strict mathematical arguments, but it should be ABSOLUTELY CLEAR to you without any arguments.



So, there are 4 remarkable points on the circle: first point is the starting point, and 3 other points 

(the points where whey meet/catch each other) are the images of the starting point, rotated 90°, 180°, and 270° along the circle.


ANSWER.  There are 4 points on the circle, where the faster cyclist catches the slower cyclist.