I need help with these two matrice problems- solving it by the Gaussian elimination method:
problem 1.)
2x + 1y - 3z = 1
3x - 1y + 4z = 6
1x + 2y - 1z = 9
Abbreviate this with an augmented matrix:
[2 1 -3 | 1]
[3 -1 4 | 6]
[1 2 -1 | 9]
Get a zero where the 3 is by
multiplying the top row by -3,
and the middle row by 2:
[-6 -3 9 | -3]
[ 6 -2 8 | 12]
[ 1 2 -1 | 9]
Add the top row to the middle row:
[-6 -3 9 | -3]
[ 0 -5 17 | 9]
[ 1 2 -1 | 9]
Get a zero where the 1 is by
multiplying the top row by 1,
and the bottom row by 6:
[-6 -3 9 | -3]
[ 0 -5 17 | 9]
[ 6 12 -6 | 54]
Add the top row to the bottom row:
[-6 -3 9 | -3]
[ 0 -5 17 | 9]
[ 0 9 3 | 51]
Get a zero where the 9 is on
the bottom row by multiplying
the middle row by 9,
and the bottom row by 5:
[-6 -3 9 | -3]
[ 0 -45 153 | 81]
[ 0 45 15 | 255]
Add the middle row to the bottom row:
[-6 -3 9 | -3]
[ 0 -45 153 | 81]
[ 0 0 168 | 336]
Rewrite as a new system of equations:
-6x - 3y + 9z = -3
-45y + 153z = 81
168z = 336
Solve the bottom equation for z:
168z = 336
z = 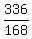 z = 2
Substitute z = 2 in the middle equation
and solve for y:
-45y + 153z = 81
-45y + 153(2) = 81
-45y + 306 = 81
-45y = -225
y =
z = 2
Substitute z = 2 in the middle equation
and solve for y:
-45y + 153z = 81
-45y + 153(2) = 81
-45y + 306 = 81
-45y = -225
y = 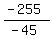 y = 5
Substitute y = 5 and z = 2 in the top equation
and solve for x:
-6x - 3y + 9z = -3
-6x - 3(5) + 9(2) = -3
-6x - 15 + 18 = -3
-6x + 3 = -3
-6x = -6
x =
y = 5
Substitute y = 5 and z = 2 in the top equation
and solve for x:
-6x - 3y + 9z = -3
-6x - 3(5) + 9(2) = -3
-6x - 15 + 18 = -3
-6x + 3 = -3
-6x = -6
x = 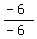 x = 1
So the solution is (x, y, z) = (1, 5, 2)
Edwin
x = 1
So the solution is (x, y, z) = (1, 5, 2)
Edwin