.
Let x be the size of the square base and h be the height of the pot, in centimeters.
Then the volume of the pot is
V = 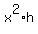 . (1)
The surface are of this pot, which has no top, is
A =
. (1)
The surface are of this pot, which has no top, is
A = 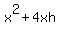 = 500 cm^2. (2)
So, we want to find optimal values of "x" and "h" to maximize the volume (1) at given restriction (2) on surface area.
From (2), we have
h =
= 500 cm^2. (2)
So, we want to find optimal values of "x" and "h" to maximize the volume (1) at given restriction (2) on surface area.
From (2), we have
h = 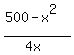 =
= 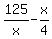 . (3)
Substitute it into (1) to get
V =
. (3)
Substitute it into (1) to get
V =  =
=  -
- 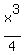 . (4)
Now we need to find a maximum value for V in formula (4) considering the volume as a function of "x" only.
For it, take the derivative of V(x) and equate it to zero
V'(x) = 125 -
. (4)
Now we need to find a maximum value for V in formula (4) considering the volume as a function of "x" only.
For it, take the derivative of V(x) and equate it to zero
V'(x) = 125 - 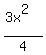 = 0.
It implies
500 = 3x^2
x^2 =
= 0.
It implies
500 = 3x^2
x^2 = 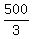 x =
x = 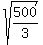 = 12.91 cm (approximately.
Then
h = (see formula (3)) =
= 12.91 cm (approximately.
Then
h = (see formula (3)) = 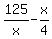 =
= 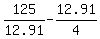 = 6.45 cm.
So, the problem is just solved.
Optimal dimensions are: the square base size of 12.91 cm and the height of 6.45 cm.
The maximum volume is
= 6.45 cm.
So, the problem is just solved.
Optimal dimensions are: the square base size of 12.91 cm and the height of 6.45 cm.
The maximum volume is 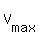 =
= 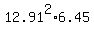 = 1075 cm^3 (approximately).
= 1075 cm^3 (approximately).
Solved.