Question 1163342: A coin with a 2-cm diameter is dropped onto a sheet of paper ruled by parallel lines that are 3 cm apart. Which is more likely, that the coin will land on a line, or that it will not?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A coin with a 2-cm diameter is dropped onto a sheet of paper ruled by parallel lines that are 3 cm apart.
Which is more likely, that the coin will land on a line, or that it will not?
~~~~~~~~~~~~~~~~~~
Notice that the radius of the coin is 1 centimeter.
We should track the position of the center of the coin at the coordinate plane relative to the lines of the grid.
Actually, we can concentrate our attention tracking the position of the center inside one fixed cell of the grid.
If the center of the coin is closer than 1 cm to some integer line of the grid, then the coin INEVITABLY will cover that line.
So, in the fixed grid cell, we should draw the square of the side size of 1 centimeter, centered at the center of this cell.
This square has the area of 1 square centimeter, while the basic square of the grid has the area of 3*3 = 9 square centimeters..
The small square is the "favorable" area: if the coin's center gets there, the coin will not cover any line of the grid.
And in opposite, if the coin's center is in the base square outside the small square, the coin will INEVITABLY cover at least one of the grid lines..
It means that the probability that the coin will not land on the line is 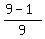 , and the probability that the coin will land on some line of the grid is  .
ANSWER. The probability that the coin will land on some grid line is  , and
the probability that the coin will not land on some grid line is .
Solved.
It is one of classic problems of the Elementary Geometric Probability theory.
For other similar solved problem, see the lesson
- Classic problem of Elementary Geometric Probability theory
in this site.
/\/\/\/\/\/\/
In my solution I assumed that the sheet of paper is classic graph paper, ruled by parallel and perpendicular lines
that are 3 cm apart making square grid.
If there are only parallel lines and there are no perpendicular lines, then the answer is different,
but the logic of the solution remains the same.
You consider then parallel lines and infinite stripes of the unit width, instead of squares.
In this case, the probability that the coin will land on some line is  ,
while the probability that it will not land is the complement  .
|
|
|
