Question 1163332: You go to the doctor and he gives you 13 milligrams of radioactive dye. After 24 minutes, 6 milligrams of dye remain in your system. To leave the doctor's office, you must pass through a radiation detector without sounding the alarm. If the detector will sound the alarm if more than 2 milligrams of the dye are in your system, how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived? Give your answer to the nearest minute.
Found 2 solutions by solver91311, Theo:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can use either of the following formulas to find your answer.
f = p * (1 + r) ^ n or f = p * e ^ (r * t)
the first formula uses discrete compounding.
the second formula uses continuous compounding.
either one will give you the answer you are looking for.
i'll do both to show you how they're done.
discrete compounding formula is f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the interest rate per period
n is the number of periods
the periods are in minutes.
first you want to find r.
then you want to find n.
to start, your formula is 6 = 13 * (1 + r) ^ 24
present value is 13
future value is 6
number of time periods is 24 minutes.
you want to solve for r
divide both sides of this equation by 13 to get:
6/13 = (1 + r) ^ 24
take the 24th root of both sides of the equation to get:
(6/13) ^ (1/24) = 1 + r
solve for r to get r = (6/13) ^ (1/24) - 1 = -.0317028303.
confirm by replacing r in the original equation with that to get:
f = 13 * (1 - .0137028303) ^ 24 = 6, confirming the value of r is good.
now that you know r, you want to solve for how long it takes to go from 13 milligrams to 2 milligrams.
the formula becomes 2 = 13 * (1 - .0317028303) ^ n
divide both sides of the equation by 13 to get:
2/13 = (1 - .01370283403) ^ n
take the log of both sides of the equation to get:
log(2/13) = log(((1 - .0317028303) ^ n)
since log(x^n) = n * log(x), this becomes:
log(2/13) = n * log(1 - .0317028303.
solve for n to get:
n = log(2/13) / log(1 - .0317028303) = 58.10118954.
13 milligrams will reduce to 2 milligrams in 58.10118954 days.
continuous compounding formula is f = p * e ^ (r * t)
f is the future value
p is the present value
r is the interest rate per time period.
t is the number of time periods.
to start, your formula is 6 = 13 * e ^ (r * 24)
you want to solve for r.
divide both sides of the equation by 13 and take the natural log of both sides of the equation to get:
ln(6/13) = ln(e ^ (r * 24))
since ln(x^n = n * ln(x), this becomes:
ln(6/13) = r * 24 * ln(e).
since ln(e) = 1, this becomes:
ln(6/13) = r * 24
solve for r to get r = ln(6/13) / 24 = -.0322162453
now you want to solve for t.
formula becomes 2 = 13 * e ^ (-.0322162453 * t)
divide both sides of the equation by 13 and take the natural log of both sides of the equation to get:
ln(2/13) = ln(e ^ (-.0322162453 * t))
since ln(x^n) = n * ln(x), this becomes:
ln(2/13) = -.0322162453 * t * ln(e)
since ln(e) = 1, this becomes:
ln(2/13) = -.0322162453 * t
solve for t to get:
t = ln(2/13) / -.0322162453 = 58.10118954
whether you used discrete compounding formula or continuous compounding formula, you get the same answer, namely 13 milligrams goes to 2 milligrams in 58.10118954 days.
your answer to the nearest minute will be 58.
these equations can be graphed.
the discrete formula becomes y = 13 * (1 - .0317028303) ^ x
the continuous formula becomes y = 13 * e ^ (-.0322162453 * x)
here is the graph.
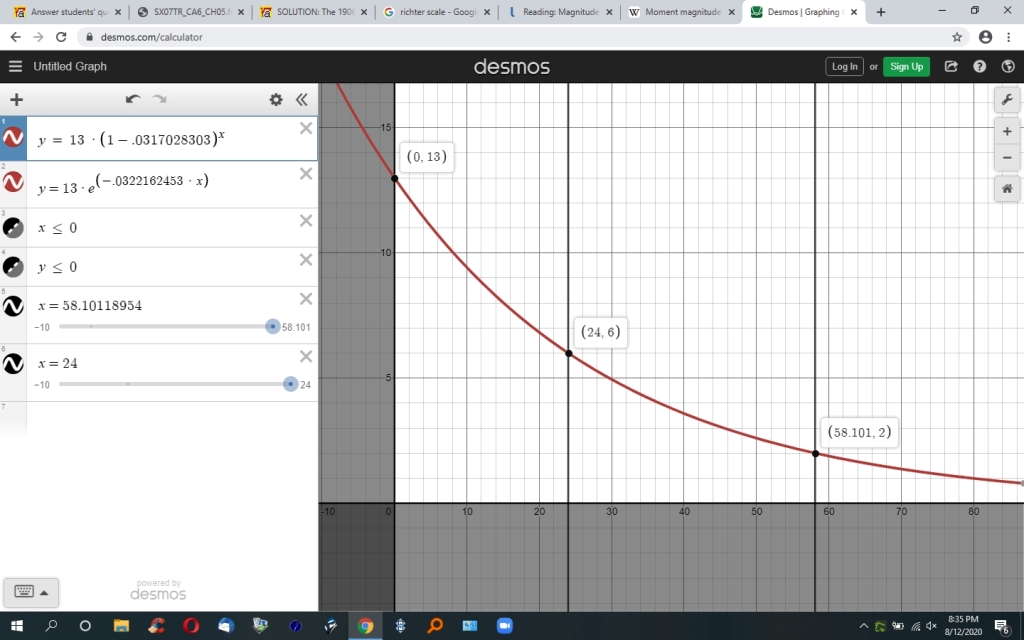
notice that the 2 equations are equivalent.
they draw the same line on the graph.
|
|
|