Question 1163322: A two-pen corral is to be built. The outline of the corral forms two
identical adjoining rectangles. If there is 120 m of fencing available and
the fence width cannot be less than 6 m, what dimensions of the corral will
maximize
the enclosed area? [round all answers to one decimal places)
In the rectangular corral Horizontal line is the length and vertical line is the width.
Thank you.
Found 3 solutions by Theo, greenestamps, Edwin McCravy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this turned my head around a few times, but i think i have it.
the corral forms two rectangles that are joined together on one side.
the total fencing available is 120 meters.
the total fencing will be 2 * the length of the enclosure plus 3 times the width of the enclosure.
the area of the enclosure is the length * width.
let:
L = length
W = width
A = area
F = fence
your equations are:
F = 2L + 3W
A = L * W
since F = 120, you get:
120 = 2L + 3W
A = L * W
from 120 = 2L + 3W, solve for L to get:
L = (120 - 3W) / 2
from A = L * W, replace L with (120 - 3W) / 2 to get:
A = (120 - 3W) / 2 * W
simplify to get:
A = 60 * W - 1.5 * W^2
rearrange the terms on the right side of thise equation by descendng order of degree to get:
A = -1.5 * W^2 + 60 * W
this is a quadratic equation in standard form where:
a = -1.5
b = 60
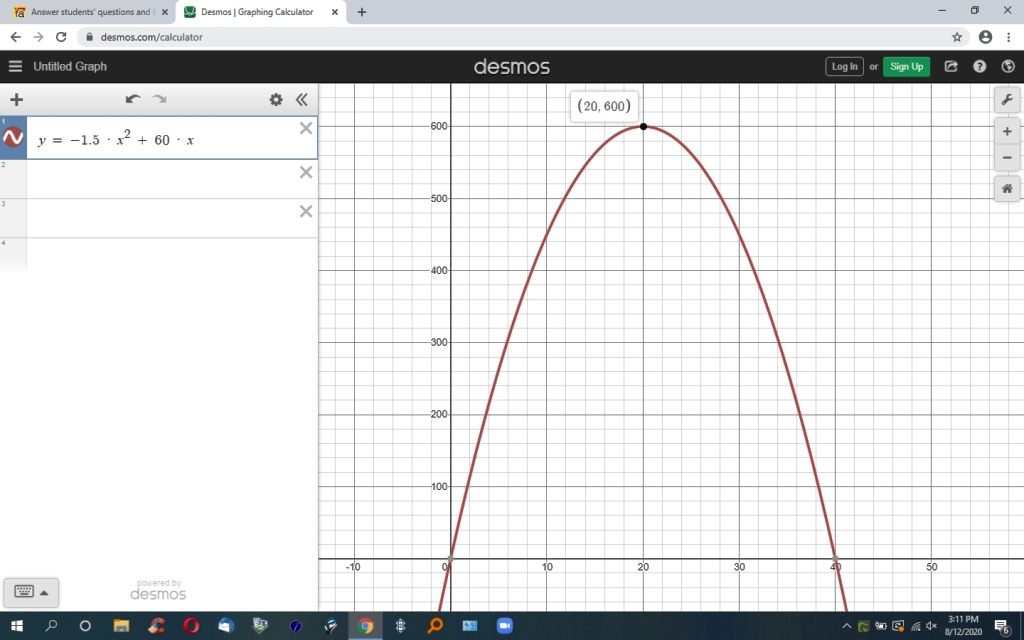
maximum value will be when W = -b/2a = 3/60 = 20
when W = 20, maximum area will be -1.5 * 20^2 + 60 * 20 = 600 square meters.
since L * W = A, then L = A / W = 600 / 20 = 30
you get:
L = 30
W = 20
F = 2L + 3W becomes F = 2*30 + 3*20 = 60 + 60 = 120, so this part checks out.
your solution is that the maximum area will be 600 square meters.
note that the perimeter is equal to 2L + 2W, making the perimeter equal to 60 + 40 = 100 meters.
you can graph the equation of area = -1.5 * W^2 + 60 * W by making area equal to y and W equal to x.
the equation becomes y = -1.5 * x^2 + 60 * x
that looks like this on the graph.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the width be x.
Since the corral is divided in half, there are three fences of length x; that's a total fence length of 3x.
The remaining length of fence, 120-3x, is the two other sides of the corral, so the length of the corral is (120-3x)/2, or 60-1.5x.
The area of the corral is then

This is a quadratic expression of the form ax^2+bx+c; its value is maximized when x is equal to -b/2a.
In this quadratic expression, 
So the width that maximizes the volume is x=20 (which satisfies the condition that it must be at least 6). And then the length is (120-3x)/2 = 30.
ANSWER: length 30 and width 20 maximizes the area.
Note that the total lengths of fencing in the two directions are equal. This is always the case, no matter how many adjacent corrals the whole corral is divided into.
For example, if you have 600 feet of fencing and you are dividing the long corral into 5 adjacent sections (using 6 sections of fence width-wise), then the maximum area is with 300 feet of fencing in each direction -- which means a length of 300/2 = 150 feet and a width of 300/6 = 50 feet.
So to an experienced problem solver, the solution to your problem would go like this:
Total fence length: 120 feet
Length of fencing in each direction: 120/2 = 60 feet
Length of corral for maximum area: 60/2 = 30 feet
Width of corral for maximum area: 60/3 = 20 feet
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
|
|
|