SOLUTION: A batch of 25 items contains 5 defective items. The batch is split in 5 groups of 5 items each. What is the probability that each group contains a defective item?

To be "successful", each group consists of exactly 4 non-defective items and
exactly 1 defective item.

We put 4 of the 20 non-defective items in the 1st group, 20C4 ways,
then we put 4 of the remaining 16 non-defective items in the 2nd group, 16C4 ways,
then we put 4 of the remaining 12 non-defective items in the 3rd group, 12C4 ways,
then we put 4 of the remaining 8 non-defective items in the 4th group, 8C4 ways,
then we put all 4 remaining non-defective items in the 5th group, 4C4=1 way,
then
we put 1 of the 5 defective items in the 1st group, 5 ways,
then we put 1 of the remaining 4 defective items in the 2nd group, 4 ways
then we put 1 of the remaining 3 defective items in the 3rd group, 3 ways
then we put 1 of the remaining 2 defective items in the 4th group, 2 ways
then we put the 1 remaining defective item in the 5th group, 1 way.

That's:



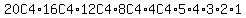"successful" ways.

Now we calculate the total number of possible ways:

We put 5 of the 25 items in the 1st group, 25C5 ways,
then we put 5 of the remaining 20 items in the 2nd group, 20C5 ways,
then we put 5 of the remaining 15 items in the 3rd group, 15C5 ways,
then we put 5 of the remaining 10 items in the 4th group, 10C5 ways,
then we put all 5 remaining items in the 5th group, 5C5=1 way,



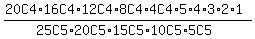That works out to be 



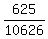
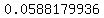
Edwin