Question 1163288: In a high school class of 100 students, 42 studied mathematics, 68 studied
psychology, 54 studied history, 22 studied both mathematics and history, 25
studied both mathematics and psychology, 7 studied history and neither
mathematics nor psychology, 10 studied all three subjects and 8 did not take
any of the three. If a student is selected at random, find the probability that
(i) he takes history and psychology but not mathematics?
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a high school class of 100 students, 42 studied mathematics, 68 studied
psychology, 54 studied history, 22 studied both mathematics and history, 25
studied both mathematics and psychology, 7 studied history and neither
mathematics nor psychology, 10 studied all three subjects and 8 did not take
any of the three. If a student is selected at random, find the probability that
(i) he takes history and psychology but not mathematics?
~~~~~~~~~~~~~~~~
We have a universal set of 100 students and the following subsets
M studied Math (42)
P studied Psychology (68)
H studied History (54)
M ∩ H studied Math and History (22)
M ∩ P studied Math and Psychology (25)
Ho studied History and neither Math nor Psychology (7) ( = H \ (H ∩ M) \ (H ∩ P) )
M ∩ P ∩ H studied all 3 subjects
U \ (M U P U H) did not take any of the three subjects (8)
So, from the condition, the union (M U P U H) of those who study at least one of the three subjects, has 100-8 = 92 students.
They want you determine the number of students who take History and Psychology but not Mathematics.
This set is (H ∩ P) \ (H ∩ P ∩ M).
To solve the problem, we will find first the number of students in the set (H ∩ P), and then will subtract 10 (which is (H ∩ P ∩ M) ) from it.
To find the number of students in the set (H ∩ P), use this remarkable identity from the elementary set theory
n(M U P U H) = n(M) + n(P) + n(H) - n(M ∩ P) - n(M ∩ H) - n(P ∩ H) + n(M ∩ P ∩ H). (1)
This identity says that the number of element in the union of any three subsets of a universal set is the sum of elements
in each subset minus the sum of elements in in-pair intersections of the subsets plus the number of elements in the triple
intersection of the three subsets.
This identity is valid for any three subsets of a universal set.
Substitute the given value into the identity (1). You will get then
92 = 42 + 68 + 54 - 22 - 25 - n(H ∩ P) + 10.
It implies
n(H ∩ P) = 42 + 68 + 54 - 22 - 25 + 10 - 92 = 35.
The last step to get the answer is to subtract 10 from 35:
the number of students who take History and Psychology but not Mathematics = n((H ∩ P) - n(M ∩ P ∩ H) = 35 - 10 = 25.
So the probability the problem asks for is P = 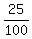 = 0.25. ANSWER = 0.25. ANSWER
The problem is just solved.
|
|
|