Question 1163270: In a high school class of 100 students, 42 studied mathematics, 68 studied
psychology, 54 studied history, 22 studied both mathematics and history, 25
studied both mathematics and psychology, 7 studied history and neither
mathematics nor psychology, 10 studied all three subjects and 8 did not take
any of the three. If a student is selected at random, find the probability that
(i) he takes history and psychology but not mathematics?
(ii) a person enrolled in history takes all three subjects?
(iii) he takes mathematics only?
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In my response, I will solve/explain part (ii) ONLY.
(ii) If a student is selected at random, find the probability that a person enrolled in history takes all three subjects?
You are given that 54 study History and 10 study all three subjects.
Therefore the probability under the question in this part is the ratio
P = 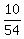 = = 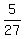 . ANSWER
In this case, you can consider the set of the 54 who study History as the sample set of events ("reduced sample set")
and the set of the 10 who study all three subjects as the favorable set,
so the probability P = . ANSWER
In this case, you can consider the set of the 54 who study History as the sample set of events ("reduced sample set")
and the set of the 10 who study all three subjects as the favorable set,
so the probability P = 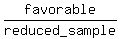 . .
This problem (ii) is a typical conditional probability problem.
In such problems, the reduction of the sample set is one of the two STANDARD methods of solution.
-------------
On conditional probability problems, see the lessons
- Conditional probability problems
- Conditional probability problems REVISITED
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability"
and "Additional problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
/\/\/\/\/\/\\/
I do not like very much when the post goes with many (more than one) problems/questions.
Then the answer EITHER becomes a mess OR is so short that prevents learning.
Therefore, if you REALLY want to LEARN from this forum (and from me personally),
do not load many questions in your post.
There is a brilliant method for solving part (i), so if you want to learn it from me,
re-post the problem again with the question (i) ONLY.
Happy learning (!)
By the way, the rules and the policy of this forum require directly, explicitly and formally
ONLY ONE PROBLEM/question per post and strictly PROHIBIT more than one.
Respect the rules and the tutors (!)
|
|
|