SOLUTION: Can you please help me with this problem? Find all the Rational zeros of each function: h(x)= {{{ x^4 + x^2 - 2 }}} this is how far i got: h(x) = {{{ x^4

Algebra ->  Rational-functions -> SOLUTION: Can you please help me with this problem? Find all the Rational zeros of each function: h(x)= {{{ x^4 + x^2 - 2 }}} this is how far i got: h(x) = {{{ x^4      Log On


   

Question 116322: Can you please help me with this problem?
Find all the Rational zeros of each function:


h(x)= 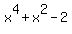+x%5E4+%2B+x%5E2+-+2+



this is how far i got:

h(x) = 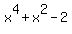+x%5E4+%2B+x%5E2+-+2+
h(-x) = +-x%5E4+%2B+x%5E2+-2+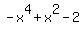
h(x) has 1 sign change
h(-x) has 2 sign changes
h(x) has 1 or 0 possible positive real roots
h(x) has 2 or more possible negative real roots.
p/q = +_ ( where the plus sign is over the minus sign in front of the number)
+_ 1, +_ 2 / +_ 1

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Your analysis has a small error.

if h%28x%29=x%5E4%2Bx%5E2-2, then h%28-x%29=%28-x%29%5E4%2B%28-x%29%5E2-2, which simplifies to the original function h%28-x%29=x%5E4%2Bx%5E2-2 because %28-1%29%5En=1 for all even n.

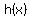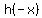Therefore, h%28x%29 has 1 sign change, so there is a maximum of 1 positive real root, and h%28-x%29 also has 1 sign change, so there is a maximum of 1 negtative real root.

This just means that you have to do some more work because the analysis doesn't say anything about whether you definitely have any real roots, nor, if you do, whether they are rational or not.

Your rational root test analysis was correct. The only possible factors of 2 are 1 and 2, and the lead coefficient is 1, so your possible rational factors are -2, -1, 1, 2.

You could just test all four of those possibilities, but I prefer to look at it this way:

Let w=x%5E2. Now if h%28x%29=x%5E4%2Bx%5E2-2, you can say that h%28w%29=w%5E2%2Bw-2

This factors rather nicely to h%28w%29=%28w%2B2%29%28w-1%29, but now we can substitute x%5E2 back in for w and get:

h%28x%29=%28x%5E2%2B2%29%28x%5E2-1%29

We know that h%28x%29=0 if and only if x%5E2%2B2=0 or x%5E2-1=0. Since we are looking for rational zeros, we can eliminate x%5E2%2B2=0 because this factor has complex roots with irrational coefficients, x=i%2Asqrt%282%29 and x=-i%2Asqrt%282%29.

But x%5E2-1=0 factors to %28x%2B1%29%28x-1%29=0 which gives us two real and rational roots, namely x=-1 and x=1.

Let's look at a graph of the original function and see if the result makes sense.

graph%28600%2C600%2C-10%2C10%2C-10%2C10%2Cx%5E4%2Bx%5E2-2%29

Yep. This is a 4th degree polynomial function, so we know that it has to have 4 roots, but the graph clearly intersects the x-axis in only two places, (-1,0) and (1,0), as we expected. That tells us that there are only 2 real roots and the other two have to be a conjugate pair of complex numbers.

Hope that helps,
John