SOLUTION: Given the following function, determine if the function is continuous at x = -2 and at x = 3. Show your work algebraically. f(x) = { (X^2-x-6)/(x+2), if x<-2 f(x) = { -5

Algebra ->  Test -> SOLUTION: Given the following function, determine if the function is continuous at x = -2 and at x = 3. Show your work algebraically. f(x) = { (X^2-x-6)/(x+2), if x<-2 f(x) = { -5       Log On


   

Question 1163182: Given the following function, determine if the function is continuous at x = -2
and at x = 3. Show your work algebraically.
f(x) = { (X^2-x-6)/(x+2), if x<-2
f(x) = { -5 , if -2≤x<3
f(x) = { (x^2-9)/(x-3) , if x≥3

Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!







John

My calculator said it, I believe it, that settles it

Answer by ikleyn(52824) About Me  (Show Source):
You can put this solution on YOUR website!
.

In vicinity of the point x= -2,  


    x^2 - x - 6 = (x-3)*(x+2),


so, after dividing by (x+2)


    f(x) = 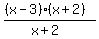%28%28x-3%29%2A%28x%2B2%29%29%2F%28x%2B2%29 = x-3  at  x < -2.


So, the limit of f(x) at x---> -2 from the left  is equal to -5.


From the other side,  f(-2) = -5, by the definition of the function f(x)  (second line).


Also, the limit f(x) at x ---> -2 from the right is equal to -5.


So, the function f(x) is CONTINUOUS at x= -2.




Next, at x= 3, the function f(x) is not formally defined, so we even can not discuss the question if it is continuous at this point.


It is NOT.

Solved, answered and explained.


/\/\/\/\/\/\/\/\/

An important post-solution note. 

    The way how the function f(x) is defined in the third line, 


        f(x) = { (x^2-9)/(x-3)  , if x≥3


    is a  HUGE mistake.   It is impossible to define a function in this way, since division by  0  at x= 3 is STRICTLY PROHIBITED.


    The correct form of this third line should be THIS


        f(x) = { (x^2-9)/(x-3)  , if x > 3.


    At x = 3, the function f(x) is UNDEFINED.