SOLUTION: help please A 6.00-m ladder is placed against a wall. If the bottom of the ladder is pushed in towards the wall at 0.400 m/s, how fast is the top of the ladder moving when the la

Imagine a coordinate plane with coordinate axes x and y (x horizontal, y vertical).


Imagine that the bottom of the ladder slides along the horizontal x-axis from some negative x-values to zero 
(from left to right).


Imagine that the top of the ladder slides along the vertical y-axis.


The length of the ladder is  d = .     (1)


Here x and y are, actually, functions of the time  x = x(t), y = y(t).


You are given that the derivative of the function x(t) over time t is 


    x'(t) = 0.4 m/s.


Square both sides of the formula (1)


    d^2 = x^2(t) + y^2(t).    (2)


Since the length of the ladder d is a constant,  d^2 is a constant, too,


Therefore, the derivative of d^2 over time is zero. 

From the other side, this derivative, from (2), is  2x*x' + 2y*y'.


Thus we have this equation


    2x*x' + 2y*y' = 0,  or,  canceling the factor 2,


    x*x' + y*y' = 0.    (3)


When y = 4.5 m above the ground, you have a right angled triangle with the hypotenuse 6 m and vertical leg of 4.5 m.

So, its horizontal leg is  x = - 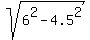 = -3.969 meters.


Now you substitute these data  x= -3.969 m,  y= 4.5 m,  x' = 0.4 m/s  into the formula (3).


You get then


    y' = - (x*x')/y = -  = 0.353 m/s.    ANSWER