.
(d) 2*|x| = y.
This formula express y as a function of x
y = 2*|x|. (d)
For every value of x, formula (d) determines y by a unique way.
In other words, for any real x as an input, formula (d) determines a unique output y.
By the definition of the notion of a function, it means that formula (d) determines y as a function of x.
(b) Same mantra works in case (b).
You start from the formula
x^2 + y = 100.
It defines the expression
y = 100 - x^2. (b)
For every value of x, the formula (b) determines y by a unique way.
In other words, for any real x as an input, formula (b) determines a unique output y.
By the definition of the notion of a function, it means that formula (b) determines y as a function of x.
(a) Same mantra works in case (a).
You start from the formula
x + 5y = 15.
It defines the expression
y =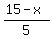 
. (a)
For every value of x, formula (a) determines y by a unique way.
In other words, for any real x as an input, formula (a) determines a unique output y.
By the definition of the notion of a function, it means that formula (a) determines y as a function of x.
(c) Same mantra DOES NOT work in case (c).
You start from the formula
x^2 + y^2 = 100.
It defines the expression
y = +/- 
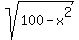. (c)
Formula (c) DOES NOT determine y by a unique way.
In opposite, to each value of x between -10 and 10, -10 < x < 10, formula (c) determines TWO values of y.
In other words, for any real x as an input, formula (c) determines TWO DIFFERENT outputs y.
By the definition of the notion of a function, it means that formula (c) DOES NOT determine y as a function of x.
In this case, y is not a function of x.
