Question 1163137: A box contained 50Cents coins and 20 cents coins in the ratio 2:3.when I took out foor 50Cents coins, exchanged them for 20 cents coins. And then put the money back in the box, the ratio became 2:7. Find the sum of money in the box.
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39631)   (Show Source):
Answer by ikleyn(52935)  (Show Source):
You can put this solution on YOUR website! .
If you take a labor to solve the system of equations, which @josgarithmetic prepared for you in his post,
you will discover at the end that the system HAS NO integer solution.
If so, it means that something is going wrong.
So, I read the problem attentively, and I came to the conclusion that the problem should be read and interpreted DIFFERENTLY.
Below is my interpretation and the full solution.
According to the condition, we can assume that initially there were 2x of the 50-cent coins and 3x of the 20-cent coins in the box.
When 4 of the 50-cent coins were taken out, the number of the 50-cent coins became (2x-4).
When these 4 50-cent coins were exchanged for 20-cent coins, 10 of 20-cent coins were returned to the box,
making the number of the 20-cent coins in the box equal to (3x+10).
So, your proportion is now
 =  .
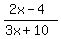From the proportion,
7*(2x-4) = 2*(3x+10)
14x - 28 = 6x + 20
14x - 6x = 20 + 28
8x = 48
x = 48/8 = 6.
So, initially in the box there were 2*6 = 12 of the 50-cent coins and
3*6 = 18 of the 20-cent coins.
Therefore, the total money in the box was 12*50 + 18*20 = 960 cents, or 9.60 dollars. ANSWER
Solved.
Answer by MathTherapy(10559)  (Show Source):
You can put this solution on YOUR website! A box contained 50Cents coins and 20 cents coins in the ratio 2:3.when I took out foor 50Cents coins, exchanged them for 20 cents coins. And then put the money back in the box, the ratio became 2:7. Find the sum of money in the box.
I agree with Tutor @IKLEYN.
Although not stated, the four (4, NOT foor) 50c coins that were removed were NOT replaced with 4 20c coins.
The four 50c coins, with a value of $2 were replaced with 20c coins worth $2, and that's 10 20c coins.
By letting the multiplicative factor be x, we get:  , and subsequently, x = 6.
So, with the multiplicative factor being 6 - leading to 12 original 50c coins worth $6, and 18 original 20c coins worth $3.60 - the sum in box = 
|
|
|
