SOLUTION: please help A rope runs through a pulley 3.05 m off the ground. One end hangs straight down and is attached to a car's engine that is being hoisted. The other end is attached 0.

According to the condition, you have a right angled triangle.


One its leg is vertical and has constant dimension  v = (3.05 - 0.61) = 2.44 meters.


The other leg is horizontal and its dimension h increases with the rate of 


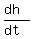     = 4 km/h = 4000/3600 m/s =  m/s.


The hypotenuse  "c"  has the length  c =   and it is the length of the rope between the pulley and 
the car's rear bumper.


The value under the question is  the derivative of "c"  over time "t"


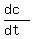     = (2*h*h'(t))/sqrt*(v^2 + h^2) = (2*h*h'(t))/sqrt*(v^2 + h^2).


You substitute the given data into the formula  and calculate 


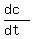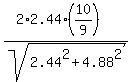     =  = 0.993808 m/s.


ANSWER.  The rope is going through the pulley at the rate of 0.993808 m/s, under given conditions.

    After reading the post. you should ask yourself:

        What is given and what they want to get from me ?



    In this problem, they want you find the derivative of the length of the hypotenuse over the time.


    As soon as you understood it, the rest is just a technique.