Question 116301This question is from textbook Elementary & Intermediate Algebra
: A pleasure boat carries passengers 10 miles upstream and then returns to the starting point. The total time of the trip(excluding the time on the ground) takes 2 hours. If the speed of the current is 2 miles per hour, find the speed of the boat in still water. Round your answer to the nearest tenth of a mile.
I need to see how you work this problem out in detail!
This question is from textbook Elementary & Intermediate Algebra
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The basic idea we will use in solving this problem is the formula that says: Distance equals
speed times time. [You can get a feel for this equation if you think, "If I go at 60 miles per
hour for 2 hours I should be 120 miles (60 * 2) from where I started.] Anyhow, we can write
this distance equation as:
.
D = S * T
.
where D represents distance, S represents speed, and T represents time.
.
The first sentence of the problem tells you that you are going to travel a distance of
10 miles upstream. Traveling upstream means that you are going against the direction that
the stream is flowing, and the actual speed of the boat is its speed in still water (call it
S) minus the speed of the current (call that s and the problem says it is 2 miles per hour).
So when you are going upstream for 10 miles at a speed of (S - 2) miles per hour our distance
equation is:
.

.
Solve this equation for T by dividing both sides of this equation by (S - 2) to get:
.

.
This T is the time it takes to go upstream for 10 miles.
.
Now let's look at the return trip. Since you are going to return to the starting point, you will
again go 10 miles. But this time you will be going in the same direction as the current is
flowing. Therefore, in this direction the speed of the boat will be its speed in still water
PLUS the speed of the current. Therefore, the actual speed of the boat is given by (S + 2)
when you go downstream. And the distance equation for this part of the trip is:
.

.
Solve this equation for the time it takes to go downstream by dividing both sides of the
equation by (S + 2) to get:
.

.
Finally, the problem tells you that the total time of the trip is 2 hours. That means that the
time going upstream ... for which we have:
.

.
plus the time to go downstream ... for which we have:
.

.
must add together to give 2 hours. In equation form this is:
.

.
You can get rid of the denominators by multiplying this entire equation (all terms on
both sides by (S - 2)* (S + 2). When you do that the equation becomes:
.

.
Cancel the terms in the denominators with their corresponding like terms in the numerators as
shown:
.

.
You are then left with:
.
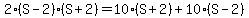
.
Notice that you can simplify this a little by dividing both sides (all terms) by 2 to get:
.

.
Now do the multiplications. First, the left side multiplies out to give:
.

.
Now multiply out the two terms on the right side:
.

.
Combine terms on the right side. Note the +10 and -10 cancel out and you are left with the
equation:
.

.
Get this into standard quadratic form by subtracting 10S from both sides to get:
.

.
The statement in the problem that tells you to round off to the nearest tenth suggests that
this problem does not have an integer solution. So let's skip trying to factor the equation
and go directly to using the quadratic formula. The quadratic formula says that for an equation
of the standard form:
.

.
The solutions will be given by the equation:
.

.
By comparing the equation we are trying to solve with the standard form we can see that
a = 1, b = -10, and c = -4. Plug these values into the appropriate places in the solutions equation
and you have:
.

.
The terms inside the radical become  . Substitute that and the equation . Substitute that and the equation
becomes:
.

.
Note that the denominator simplifies to 2 and the -(-10) is +10. Substituting these values
results in the further simplified form:
.

.
Calculator time. The square root of 116 is 10.77032961. Substitute that value and you have:
.

.
Look carefully at the numerator. If you use the minus sign the resulting numerator will
be a negative value ... and it doesn't make sense to have a negative speed. So let's just
go with the positive sign and this makes the equation:
.

.
This means that the speed of the boat in still water is (rounding to the nearest tenth) 10.4
miles per hour.
.
Check ... in going upstream the time is equal to distance divided by speed and that is:
.
 hours. hours.
.
in going downstream the time is:
.
 hours. hours.
.
So the total round trip time is 1.19 + 0.81 = 2 hours ... just as it should be. The answer
checks so we can say that the speed of the boat in still water is 10.4 miles per hour.
.
Hope this helps you understand the problem and how you can get the answer.
.
|
|
|