Question 1162983: Two marksmen shoot at a target simultaneously. Shooter A is known to have a 70% chance
of hitting the target on any attempt. Person B has 40% accuracy. After the target is hit for the first time,
it is revealed that A shot 5 shots while B shot 12. What is the probability that it was A who hit the target?
What is the probability that person B hit the target? (Assume that accuracies of the shots remain the same
and are independent of other shots by either person.)
Answer by ikleyn(52783)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two marksmen shoot at a target simultaneously. Shooter A is known to have a 70% chance
of hitting the target on any attempt. Person B has 40% accuracy. After the target is hit for the first time,
it is revealed that A shot 5 shots while B shot 12. What is the probability that it was A who hit the target?
What is the probability that person B hit the target?
(Assume that accuracies of the shots remain the same and are independent of other shots by either person.)
~~~~~~~~~~~~~~~~~
We are given that EITHER A hits the target first time at his 5-th shot,
OR B hits the target first time at his 12-th shot,
but we do not know exactly who did it first, A or B.
Also notice that this "OR" is EXCLUSIVE: either A or B, but not both.
The probability that A hits the target first time with his 5-th shoot AND B do not hit target with his 12 shoots is
P(A, 5+; B, 12-) = 0.7*(1-0.7)^4 * (1-0.4)^12 = 0.7*0.3^4 * 0.6^12 = 0.00001234.
The probability that B hits the target first time with his 12-th shoot AND A do not hit target with his 5 shoots is
P(B, 12+; A, 5-) = 0.4*(1-0.4)^11 * (1-0.7)^5 = 0.4*0.6^11 * 0.3^5 = 0.00000353.
The probability that it is A who hits the target first is
P(A, 5+; B, 12-) / ( P(A, 5+; B, 12-) + P(B, 12+; A,5-) ) = 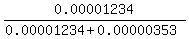 = 0.7778.
The probability that it is B who hits the target first is
P(B, 12+; A, 5-) / ( P(A, 5+; B, 12-) + P(B, 12+; A,5-) ) = = 0.7778.
The probability that it is B who hits the target first is
P(B, 12+; A, 5-) / ( P(A, 5+; B, 12-) + P(B, 12+; A,5-) ) = 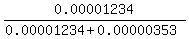 = 0.2222.
ANSWER. The probability that A hits the target first is 0.7778.
The probability that B hits the target first is 0.2222, = 0.2222.
ANSWER. The probability that A hits the target first is 0.7778.
The probability that B hits the target first is 0.2222,
Solved.
|
|
|