SOLUTION: 1) Lets look at some examples of different functions. Each of the following functions has a zero located at x = 3. For each function, determine if the function’s graph crosses or

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 1) Lets look at some examples of different functions. Each of the following functions has a zero located at x = 3. For each function, determine if the function’s graph crosses or      Log On


   

Question 1162807: 1) Lets look at some examples of different functions. Each of the following functions has a zero located at x = 3. For each function, determine if the function’s graph crosses or only touches the x-axis at x = 3.


f(x)=x(x-3)^2
g(x) = x(x+2)(x-3)
h(x)=(x-3)^3
2) . Do some additional examples for yourself using functions you create yourself by multiplying two or three linear factors so that there are clear zeros. Feel free to use squared or cubed linear factors like f(x) and h(x) above. Is there a pattern to when the graph of the function only touches the x-axis and when it actually crosses it?


3)The degree of a polynomial can be found by fully expanding the polynomial. Once this is done, look at the variable in the polynomial with the largest exponent. This exponent is the degree of the polynomial. The leading coefficient of a polynomial is the coefficient of the term with the largest exponent. Look at the graphs of each of the examples you have worked with so far and expand them using multiplication. Do you notice a pattern of when a graph starts below or above the x-axis? Do you notice a pattern when a graph ends below or above the x-axis?


4)Create a function that does the following: • It touches the x-axis at two points, x = -3 and x = 1 • It begins above the x-axis • It ends below the x-axis.
Found 3 solutions by solver91311, Boreal, greenestamps:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


The -axis is tangent to the graph of all polynomial functions that have an even number of identical factors.

So the -axis is tangent to the graph of at , but the graph of crosses the -axis at and the graph of crosses the -axis at .


John

My calculator said it, I believe it, that settles it

Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
f(x)=x(x-3)^2 roots at 0 and 3, with a bounce at 3. Crosses and touches
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2Cx%2A%28x-3%29%5E2%29
g(x)=x(x+2)(x-3), roots at 0,-2, 3 crosses
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2Cx%2A%28x%2B2%29%28x-3%29%29
H(x)=(x-3)^3 crosses at x=3
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C%28x-3%29%5E3%29
4. -(x+3)(x-1)^2. This is a cubic, so making it negative will have the beginning positive and the end negative. Put in a bounce as the last pair of roots, and the function crosses once and touches.
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C-%28x%2B3%29%28x-1%29%5E2%29

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Two earlier responses have answered only parts of your question....

The graphs from the first tutor answer part 1.

The response from the second tutor answers part 2. But I will expand on that part.

The answer to part 2 is this: If a linear factor occurs an odd number of times, the graph crosses the x-axis; if a linear factor occurs an even number of times, the graph just touches the x-axis.

It is easy to see that that makes sense.

The sign of the function depends on the signs of the linear factors. Imagine "walking" along the x-axis and passing the point corresponding to one of the linear factors.

If the linear factor occurs an odd number of times, then the signs change for an odd number of linear factors; and that means the sign of the function changes.
If the linear factor occurs an even number of times, then the signs change for an even number of linear factors; and that means the sign of the function does NOT change.

part 3)....

The short answer -- which should be easy to understand after parts 1 and 2, is this:

even degree; leading coefficient positive <--> starts and ends above the x-axis
even degree; leading coefficient negative <--> starts and ends below the x-axis
odd degree; leading coefficient positive <--> starts below the x-axis; ends above the x-axis
odd degree; leading coefficient negative <--> starts above the x-axis; ends below the x-axis

part 4)....

From part 3, we know the function has to be odd degree with negative leading coefficient.

With only two roots -3 and 1, and therefore only two linear factors (x+3) and (x-1); and needing an odd degree for the function, one of the factors has to occur an even number of times and the other an odd number of times.

Let's have fun and make the (x-1) factor occur twice and the (x+3) factor occur three times.

And remember we need a negative leading coefficient.

So a function that satisfies all the requirements is

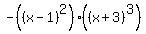
-%28%28x-1%29%5E2%29%28%28x%2B3%29%5E3%29

A graph....

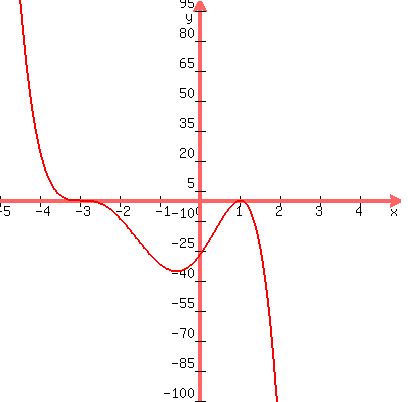
graph%28400%2C400%2C-5%2C5%2C-100%2C100%2C-%28%28x-1%29%5E2%29%28%28x%2B3%29%5E3%29%29

begins above the x-axis...
crosses the x-axis at -3...
touches the x-axis at 1...
ends below the x-axis