SOLUTION: Britney wants to bake at most 10 loaves of bread for a bake sale. She wants to make banana bread that sells for Php 50 each loaf and carrot bread for Php 60 each and make at leas

Let x = the number  of banana bread loaves,

    y = the number  of carrot bread loaves.


Then your inequalities are


      x +   y <= 10      (1)    (counting loaves)

    50x + 60y >= 580     (2)    (counting money)


You have a system of inequalities consisting of two inequalities, that must be held simultaneously.


Use the graphical method to solve it.


In a coordinate plane (x,y) draw the line  y = 10-x, representing first inequality.

Draw the second line  y =  = 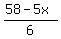, representing second inequality.


These lines are shown in my plot below.


    


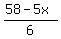    Plot y = 10-x  (red),   y =   (green)


The solution set to your inequalities are the points with integer coordinates x and y, that are

below or on the red line and above or on the green line.


As you see from the plot, there are not so many such points (solutions).


The solutions are the points  (x,y) = (0,10) and (1,9).


So, the examples of solutions, the problems asks for are

    a)  0 banana, 10 carrot loaves

    b)  1 banana, 9 carrot  loaves.