SOLUTION: A box holds 12 gold widgets, 20 black widgets, and some number of white widgets. Ahmed reaches into the box and randomly selects one widget. If the probability that Ahmed selects a

Algebra ->  Probability-and-statistics -> SOLUTION: A box holds 12 gold widgets, 20 black widgets, and some number of white widgets. Ahmed reaches into the box and randomly selects one widget. If the probability that Ahmed selects a      Log On


   

Question 1162649: A box holds 12 gold widgets, 20 black widgets, and some number of white widgets. Ahmed reaches into the box and randomly selects one widget. If the probability that Ahmed selects a white widget is 1/𝑝, determine the sum of all possible integer values of 𝑝.
Answer by ikleyn(52908) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let "w" be the number of white widgets.


Then from the condition, you have this equation


    w%2F%2812%2B20%2Bw%29 = 1%2Fp.


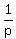It gives


    pw = 12 + 20 + w,   or

    (p-1)*w = 12 + 20 = 32.


So, "p-1" is one of the divisors of the integer number 32.


The possible divisors are p-1 = 1, 2, 4, 8, 16 and/or 32  (all degrees of 2, from 0 to 5).


So, there are 6 possible integer values for p,  2, 3, 5, 9, 17 and 33.    ANSWER

Solved.