Question 1162646: for $20 you purchase a ticket that gives you a chance to win a $6000 boat. there are $2000 tickets being sold. what is the expected value of buying a ticket?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52855)   (Show Source):
You can put this solution on YOUR website! .
In all, there are 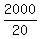 = 100 tickets.
The probability to win is  = 0.01.
The expected value of purchased ticket is 0.01*6000 - 20 = 60 - 20 = 40 dollars. ANSWER
Pretty benefiting purchase (!)
Urgently buy all 100 tickets for $2000; win the boat costing $6000 and then sell it via your web-site,
earning the difference of $4000 to your pocket.
/\/\/\/\/
Tutor @greenestamps often allows himself to comment my solutions by arbitrary ways.
When I solved this problem, I did not assume that it is nonsensical - I simply solved it "as is":
exactly as it was worded, printed, posted and presented.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Presumably the problem is supposed to say that the number of tickets sold is 2000 -- not that the total cost of the tickets is $2000.
If the total cost of the tickets is $2000, then the problem is nonsensical -- as the other tutor pointed out.
In an expected value problem like this, you can find the expected value of one ticket by comparing the total prizes to the total cost of the tickets.
The total cost of the tickets is 2000($20) = $40,000; the total prize value is $6000.
The total value to the ticket buyers is then $6000-$40,000 = -$34,000; and then the expected value of one ticket is -$34,000 divided by 2000, which is -$17.
ANSWER: The expected value of a ticket is -$17.
|
|
|
