Question 1162620: Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%.The total income from all 3 investments is $1600. The income from the 5% and 6% investments is the same as the income from the 8% investment. Find the amount invested at each rate
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%.
The total income from all 3 investments is $1600. The income from the 5% and 6% investments is the same
as the income from the 8% investment. Find the amount invested at each rate.
~~~~~~~~~~~~~~
In this problem, the key phrase is that saying
The income from the 5% and 6% investments is the same as the income from the 8% investment.
It means that the income from 8% investment is half of the total interest of $1600, i.e. $800.
Next, since the interest of the 8% investment is $800, it means that the amount of the 8% investment is 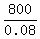 = 10000 dollars.
Thus, we just know that the 8% investment was $10000; hence, the parts invested at 5% and 6%, make the rest $25000-$10000 = $15000.
Doing in this way, we just reduced the problem from 3 unknowns to only 2,
and the rest of the problem can be solved using one unknown, only.
Let x be the amount invested at 6%; then the amount invested at 5% is (15000-x) dollars.
The total interest equation for these two parts is
0.05*(15000-x) + 0.06x = 800 dollars (another half of $1600).
From this equation,
x = 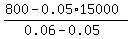 = 5000.
Thus we have the ANSWER : $5000 was invested at 6%; 15000-5000 = 10000 dollars was invested at 5% and $10000 was invested at 8%.
CHECK. 0.06*5000 + 0.05*10000 + 0.08*10000 = 1600 dollars,
which is precisely correct total interest.
Solved.
---------------
The major lesson to learn is that the problem can be solved using one unknown ONLY (!)
See the lessons
- Advanced word problems to solve using a single linear equation
- HOW TO algebreze and solve these problems using one equation in one unknown
in this site and find there other numerous similar solved problems.
Answer by greenestamps(13214)  (Show Source):
You can put this solution on YOUR website!
There was $800 of income from the 8% investment, and there was $800 of income combined from the 5% and 6% investments.
$800 income from an 8% investment means the amount invested at that rate was $10,000.
So the combined amounts invested in the 5% and 6% investments was $15,000.
$15,000 all invested at 5% would yield $750 income; all at 6% would yield $900 income.
The actual income from those two investments, $800, is one-third of the way from $750 to $900. That means 1/3 of the remaining $15,000 was invested at the higher rate. So $5000 at 6% and $10,000 at 5%.
ANSWER: $10,000 at 8%; $10,000 at 5%, and $5000 at 6%.
CHECK:
.08(10,000)+.05(10,000)+.06(5000) = 800+500+300 = 1600
|
|
|
