The reason to find the eigenvectors is to diagonalize the matrix, so after
finding the eigenvectors, we'll go ahead and diagonalize the matrix A so we
can check to see that they are the correct eigenvectors.
We are given the eigenvalues. For
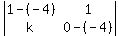
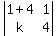
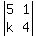
So k=20.
We could do the same with the other eigenvector, but it will also give k=20.
So now we have
To diagonalize A we want to find matrices D and S so that we can write A as
where D is the diagonal matrix with the two eigenvalues on the
main diagonal:
and the matrix S is
where the V's are the two column eigenvectors for the two eigenvalues
We find V1 which is the eigenvector for the eigenvalue λ=-4.
We find solutions for
Divide thru by -18
We can take x1=1 and x2=-5
So
Now we do the same for the other eigenvalue
---
We find solutions for
We can take x1=1 and x2=4
So
Now we have done that was asked for, for we have the two eigenvectors. So we
can stop here.
-------------------------------------
But let's check to make sure this matrix whose columns are the two
eigenvectors:
provide the correct diagonalization of A.
Since the determinant of S is 9, to find S-1 we only need to swap the
elements on the the main diagonal and change the signs of the other two
elements, then multiply by 1/9:
Then if we've done everything right, this will be true:
So we check to see if this is the correct diagonalization of A:
So the eigenvalues are correct because
is the correct diagonalization of A.
Edwin
