Question 1162427: Sketch the situation if necessary and use related rates to solve.
A 5 ft tall person walks toward a wall at a rate of 4 ft/s. A spotlight is located on the ground 40 ft from the wall.
a) How fast (in ft/s) does the height of the person's shadow on the wall change when the person is 5 ft from the wall?
b) What is the rate (in ft/s) at which the shadow changes when the person is 5 ft from the wall, if the person is walking away from the wall at a rate of 4 ft/s?
Note: part b is the hardest for me, would you please explain it to me. Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE GEOMETRY, RATIOS, PROPORTIONS, AND RATES ASPECT:
  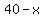   are base and height lengths of the two similar right triangles, in feet. are base and height lengths of the two similar right triangles, in feet.
 --> -->  --> --> 
With the person at  feet from the wall, feet from the wall,
the shadow height (in feet) is   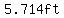
With the person at  feet from the wall, feet from the wall,
the shadow height (in feet) is  
With the person at  feet from the wall, feet from the wall,
the shadow height (in feet) is  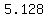
NOTE:
This is a calculus problem involving derivatives.
It requires understanding rates and proportions. and geometry of similar triangles, but to truly understand the problem more advanced math is needed.
I will explain the problem with and without derivatives.
If you are not in a calculus class, your teacher may or may not realize the complexity of the problem. Maybe your teacher realizes, but is happy with partial understanding.
Pretending that advanced math is not required, you can get results for the problem that are not correct, but are close enough.
WITHOUT CALCULUS:
As the person walks towards the wall for a second, the distance to the wall goes from 5 ft to 1 ft,
and the person's shadow's length goes from 5.714 ft to 5.128 ft.
The average rate of change over that 1-second period is
 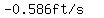
As the person walks towards the wall for 0.1 second, the distance to the wall in ft goes from  to to  , ,
and the person's shadow's length (in ft) goes from 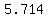 to to
 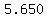
The average rate of change over that 0.1-second period is
 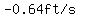
As the person walks towards the wall for 0.01 second, the distance to the wall in ft goes from  to to  , ,
and the person's shadow's length (in ft) goes from 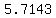 to to
 
The average rate of change over that 0.1-second period is
  . .
I would say that is an accurate enough answer.
The problem is that the rate of change is constantly changing,
just like my speed does when I drive through during the downtown lunch rush. My speed is zero at times, but as I a light turns green in front of me, I may start going faster and faster. As we consider shorter and shorter intervals the successive results get closer to each other and to the rate at the instant the person is 5 ft from the wall. That is why the policeman clocks cars for short periods of time to get accurate instant speed readings.
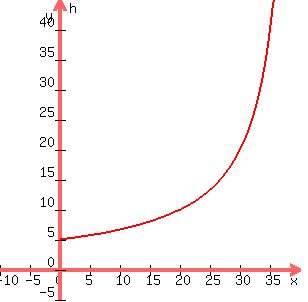
As the person walks away from the wall for a second, the distance to the wall goes from 5 ft to 9 ft,
and the person's shadow's length goes from 5.714 ft to 6.452 ft.
The average rate of change over that 1-second period is
 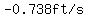
As the person walks away from the wall for 0.1 second, the distance to the wall in ft goes from  to to  , ,
and the person's shadow's length (in ft) goes from 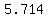 to to
 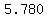
The average rate of change over that 0.1-second period is
 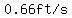
As the person walks away from the wall for 0.01 second, the distance to the wall in ft goes from  to to  , ,
and the person's shadow's length (in ft) goes from 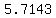 to to
 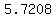
The average rate of change over that 0.1-second period is
  . .
I would say that is an accurate enough answer.
WITH CALCULUS:
The shadow height (h) is a function of the distance (x) between the person and the wall,
 , ,
and that distance (x) is a function of time {t).
Rates of change are what calculus teachers call derivatives.
The rate of change of h with t is 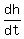 . .
It is the product of
the rate of change of h with x, 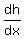 and and
the rate of change of x with t  : :

 . .
As  is a linear function of is a linear function of  when the person is walking at a constant rate, when the person is walking at a constant rate,
with  in seconds, when the person is walking at 4 ft/s, in seconds, when the person is walking at 4 ft/s,
 (ft/s) when the person is walking towards wall, and (ft/s) when the person is walking towards wall, and
 (ft/s) when the person is walking away from the wall. (ft/s) when the person is walking away from the wall.
For  (ft) (ft)  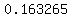 (no units, because it's a ratio of distances). (no units, because it's a ratio of distances).
 when the person is walking towards wall, and when the person is walking towards wall, and
 when the person is walking away from the wall. when the person is walking away from the wall.
|
|
|