Question 1162139: The Seattle airport is 205 km, 19° E of S from Vancouver airport. The trip takes 1 hour by plane. If there is a strong 92 km/h wind blowing towards 40° N of E, what is the magnitude and direction of the plane’s velocity so that it makes the trip in 1 hour.
Answer by ikleyn(52872)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I am not a pilot and never learned these notations.
But I have a common sense, instead, and will try to explain you the method of solution.
I hope that, knowing the method, you will be able to complete the solution on your own (as it is your SUPERIOR goal, I hope).
In this problem, we need to distinct the earth-speed of the plane 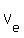 from its air-speed from its air-speed 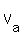 .
The earth-speed .
The earth-speed 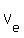 is the speed relative the Earth surface, which is considered as flat and unmoved
(we neglect the spherical form of the Earth and neglect its rotation about its axis).
The air-speed is the speed relative the Earth surface, which is considered as flat and unmoved
(we neglect the spherical form of the Earth and neglect its rotation about its axis).
The air-speed 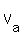 is the speed of the plane relative the air (which is blowing, in the second scenario).
The earth-speed is the same in both scenarios: its magnitude is 205 kilometers per hour
and its direction is " 19° E of S from Vancouver airport ".
+------------------------------------------------------------------+
| |
| It is the first key point to understand to solve the problem. |
| |
+------------------------------------------------------------------+
The problem asks us to find the air-speed in the second scenario: its magnitude and its direction.
Next, from the given data, you can express the speed of the wind is the speed of the plane relative the air (which is blowing, in the second scenario).
The earth-speed is the same in both scenarios: its magnitude is 205 kilometers per hour
and its direction is " 19° E of S from Vancouver airport ".
+------------------------------------------------------------------+
| |
| It is the first key point to understand to solve the problem. |
| |
+------------------------------------------------------------------+
The problem asks us to find the air-speed in the second scenario: its magnitude and its direction.
Next, from the given data, you can express the speed of the wind 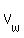 via its components via its components
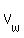 = ( = ( 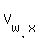 , ,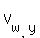 ), ), 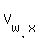 = 92*cos(a), = 92*cos(a), 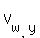 = 92*sin(a),
where " a " is that angle " 40° N of E ".
The plane air-speed = 92*sin(a),
where " a " is that angle " 40° N of E ".
The plane air-speed 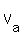 , with the components , with the components 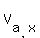 and and 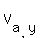 , should satisfy this vector equation , should satisfy this vector equation
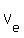 = = 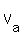 + + 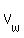 . (1)
+------------------------------------------------------------------+
| |
| Equation (1) is the second key point to the problem' solution. |
| |
+------------------------------------------------------------------+
In this equation, you know . (1)
+------------------------------------------------------------------+
| |
| Equation (1) is the second key point to the problem' solution. |
| |
+------------------------------------------------------------------+
In this equation, you know 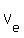 and and 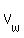 (via their components) and do not know (via their components) and do not know 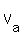 , which is the major unknown.
But having this equation (1) and components of the known vectors , which is the major unknown.
But having this equation (1) and components of the known vectors 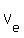 and and 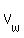 , you can calculate
the components of the vector , you can calculate
the components of the vector 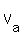 .
By moving in this way, in accordance with my instructions, you will be able to solve the problem COMPLETELY on your own. .
By moving in this way, in accordance with my instructions, you will be able to solve the problem COMPLETELY on your own.
Happy calculations (!)
and remember that you NOWHERE will find so clear explanations and instructions.
|
|
|