Question 1161853: Formula for question (a): nPr=n!/r!(n-r)! Assume a class has 24 members.
(a)How many 4-person committees can be formed out of a class of 15?
Formula for (b): The number of combinations of n objects taken r at a time is given by the formula nCr=n!/r!(n-r_!
(b)How many committees of 10 people can be chosen?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have a wrong formula, and formulas are not good for brain health.
For a student, understanding and reasoning is best for brain health.
You cannot raise wise students feeding them formulas.
(You can figure out by yourself how to feed babies for best brain health).
However, to communicate with computers, calculators, and math teachers
we need a little vocabulary/symbols. (More of that later).
The symbol 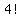 represents represents  , ,
a product with the first 4 counting numbers as factors.
We call it "factorial of 4" or "4 factorial".
My calculator has "x!" as a function,
but factorial is used for positive integers,
although we extend it beyond  to to  . .
(a) I understand that when we pick  students for a committee out of a class of students for a committee out of a class of  students, students,
we just need a group/set of  students. students.
We can list them in any order and it is the same committee
with all students equally important for now.
They can distribute their roles and responsibilities among themselves later.
We could instead make an ordered list,
where the first named is the president of the committee,
the second one is the secretary/note-taker,
the third is the treasurer,
and the last one brings the donuts to the meetings.
In that case the same 4 people mentioned in different order make a different list.
When we make lists of  people out of people out of  available to choose from, available to choose from,
we have  choices for the first name in the list. choices for the first name in the list.
Afterwards, for each of those  choices, choices,
we will have  remaining choices for a second name (the remaining choices for a second name (the  not yet chosen students). not yet chosen students).
Then, we will have  choices for the third name, choices for the third name,
and  choices for the fourth. choices for the fourth.
All in all, we could make  lists. lists.
That is not 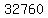 different sets of students, different sets of students,
because each set of 4 students can be listed  different ways Different orders). different ways Different orders).
We will find each different set of 4 students repeated as  times in those times in those 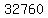 lists. lists.
Those 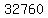 lists represent only lists represent only
 different committees. different committees.
(b) For a list of 10 students out of a class of  there are there are
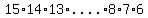 different possibilities different possibilities
That is a product of  factors that are the numbers from 1 to 15, except the first factors that are the numbers from 1 to 15, except the first  numbers. numbers.
We would tell a computer or a calculator to calculate that as computer could see that as
 . .
Each set of  students can be written in students can be written in  different orders as different orders as  different lists, different lists,
so the  different lists represent different lists represent
 . .
MORE symbols and vocabulary:
My (cheap) scientific calculator has keys for the functions 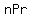 and and 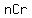 . .
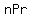 (with (with  , of course) represents , of course) represents
the number of different permutations (lists) of  items that can be made items that can be made
out of a total of  different items. different items.
It is called permutations of n taken r at a time because the same r items in different order make a different list/permutation.
The formula to calculate that number is
 , where , where
 is the product of the is the product of the  consecutive integers from consecutive integers from  to to  , and , and
 is the product of the is the product of the 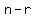 consecutive integers from consecutive integers from  to to 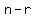 , ,
(except that we define  for consistency). for consistency).
 represents the number of list permutations of n items represents the number of list permutations of n items
that we can make using all n items at a time (for each list).
We just call it permutations of n, but 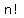 is shorter and more direct. is shorter and more direct.
  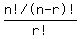   represents the number of different sets/combinations you can make represents the number of different sets/combinations you can make
by picking  items out of items out of  available items. available items.
We use "C" in that symbol for combinations,
meaning that we consider {lettuce,tomato,pickle} the same
set/combination of 3 burger toppings as {tomato,pickle,lettuce} .
|
|
|