SOLUTION: If A= 4 4 −2 −1 0 1 3 6 −1 , show that A^2 = A + kI for some constant k, where I is the unit matrix of order 3. Hence find the inverse matrix A^−1 .

Algebra ->  Matrices-and-determiminant -> SOLUTION: If A= 4 4 −2 −1 0 1 3 6 −1 , show that A^2 = A + kI for some constant k, where I is the unit matrix of order 3. Hence find the inverse matrix A^−1 .      Log On


   

Question 1161807: If
A=
4 4 −2
−1 0 1
3 6 −1
,
show that A^2 = A + kI for some constant k, where I is the unit matrix of order 3. Hence
find the inverse matrix A^−1
.
Answer by ikleyn(52832) About Me  (Show Source):
You can put this solution on YOUR website!
.

Having this assignment, the student SHOULD NOT think.


He (or she) simply MUST KNOW how to multiply matrices - - - and calculate A^2, directly and explicitly, on his (or her) own.


At this step, there is NOTHING to ask the tutors for help - - - it is THE STUDENTS' job.


When you establish this equality  A^2 = A + kI,  you will find the value of "k".


What follows, is simple.


This equality  A^2 = A + kI, can be written in the form

    A^2 - A = kI;


then factored

    A*(A-I) = kI


then presented in the form

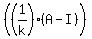    A.%28%281%2Fk%29%2A%28A-I%29%29 = I,


and it means that the inverse matrix is equal

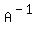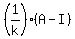    A%5E%28-1%29 = %281%2Fk%29%2A%28A-I%29.


So, your steps are


(a)  to establish / (to check) that  A^2 = A + kI  and find the value of "k".

     This step you MUST make on your own, as I just explained you.


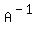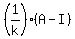(b)  Then the inverse matrix to A is  A%5E%28-1%29 = %281%2Fk%29%2A%28A-I%29.

-------------

Now, when I explained you every your step, I am waiting for your "THANKS" for my instructions.