Question 1161657: A ship that can cruise at 65 km/h in still waters, set course south-west. It is driven off course by a current flowing W 21° N at a rate of 16 km/h.
Calculate the resultant velocity in magnitude and direction
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The way I understand the problem the ship started going south-west in still water, which I would represent like this:
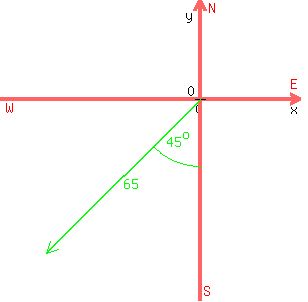
I would decompose the ship-still water velocity vector 
into components in the x- and y-directions:
 and and  . .
According to my understanding directions are given as angles measured clockwise from North,
or as acute angles from the North or South directions, with N or S followed by the angle and then the direction.
In the second case,    would mean a direction forming a would mean a direction forming a  angle from North in the direction of West, like this angle from North in the direction of West, like this

However, the    in this problem may mean a in this problem may mean a  angle from West in the direction of North, like this angle from West in the direction of North, like this

In that case the x- and y-components of the current vector  are are
 and and  , ,
and the situation would look like this

Then, the components of ship resultant velocity vector 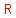 would be would be
 and and  . .
A way to calculate the magnitude of that resultant is using the Pythagorean theorem
 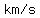
The angle  if forms with the x-axis is such that if forms with the x-axis is such that
 , which corresponds to , which corresponds to 
If the current was designated as   
because it was  North from West, North from West,
then 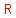 is is 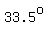 South from West, South from West,
and should be called  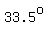  . .
|
|
|