.
(1) Use the formula for the area of the partallelogram
area = 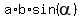 ,
where "a" and "b" are any two adjacent sides of the parallelogram and
,
where "a" and "b" are any two adjacent sides of the parallelogram and  is the angle concluded between them.
From this formula,
is the angle concluded between them.
From this formula,  =
=  = 0.5.
(2) Hence, the acute angle of the parallelogram is 30°, and the obtuse angle is 150°.
The cosine of the obtuse angle is cos(150°) = -
= 0.5.
(2) Hence, the acute angle of the parallelogram is 30°, and the obtuse angle is 150°.
The cosine of the obtuse angle is cos(150°) = -  then.
(3) Now apply the cosine rule
the length of the longer diagonal =
then.
(3) Now apply the cosine rule
the length of the longer diagonal = 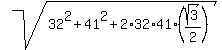 =
=  = 70.55 feet. ANSWER
= 70.55 feet. ANSWER
Solved.